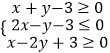题目内容
【题目】函数f（x）= 
（常数a∈Z）为偶函数且在（0，+∞）是减函数，则f（2）=
【答案】
【解析】解：∵函数f（x）= 
（常数a∈Z）在（0，+∞）是减函数，∴a2﹣2a﹣3＜0，解得﹣1＜a＜3，
∵a∈Z，∴a=0，1，2，
若a=0，则f（x）=x﹣3 ， 为奇函数，不满足条件．
若a=1，则f（x）=x﹣4 ， 为偶函数，满足条件．
若a=2，则f（x）=x﹣3 ， 为奇函数，不满足条件．
故a=1，f（x）=x﹣4= 
，
则f（2）= ，
所以答案是：
【考点精析】关于本题考查的奇偶性与单调性的综合，需要了解奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案．
练习册系列答案
备战中考寒假系列答案
相关题目
