题目内容
4.已知双曲线C的中心在坐标原点,焦距2c=6,一条准线方程为x=2(1)求双曲线C的方程;
(2)若双曲线C的渐近线与圆(x-3)2+y2=r2(r>0)相切,求实数r的值.
分析 (1)由题意可得c=3,$\frac{{a}^{2}}{c}$=2,解得a,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$,即可得到双曲线的方程;
(2)求得渐近线方程,由直线和圆相切的条件:d=r,运用点到直线的距离公式,计算即可得到r.
解答 解:(1)焦距2c=6,一条准线方程为x=2,
可得c=3,$\frac{{a}^{2}}{c}$=2,
解得c=3,a=$\sqrt{6}$,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$,
则双曲线的方程为$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1;
(2)双曲线C的渐近线为y=±$\frac{\sqrt{2}}{2}$x,
由渐近线与圆(x-3)2+y2=r2(r>0)相切,
可得圆心(3,0)到渐近线的距离为r,
即d=$\frac{|\frac{3\sqrt{2}}{2}|}{\sqrt{1+\frac{1}{2}}}$=r,可得r=$\sqrt{3}$.
点评 本题考查双曲线的方程和性质,主要考查渐近线方程的运用,以及直线和圆相切的条件:d=r,考查运算能力,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6.已知集合A={x|2x2-x-1≤0},集合B={x|y=$\frac{2ln({3}^{x}-1)}{(x-1)^{2}}$},则A∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
16.己知cos31°=a,则sin239°•tan149°的值是( )
| A. | $\frac{1-{a}^{2}}{a}$ | B. | $\sqrt{1-{a}^{2}}$ | C. | $\frac{{a}^{2}-1}{a}$ | D. | -$\sqrt{1-{a}^{2}}$ |
14.若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2,当x1≠x2时,恒有(x1-x2)[f(x1)-f(x2)]<0,则称函数f(x)为“优美函数”,则下列函数中是“优美函数”的是( )
| A. | f(x)=ex+e-x | B. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | ||
| C. | f(x)=lg($\sqrt{{x}^{2}+1}-x$) | D. | f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≥0}\\{-{x}^{2},}&{x<0}\end{array}\right.$ |
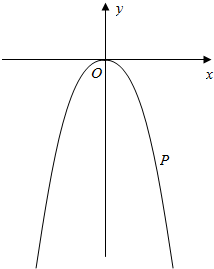 已知抛物线y=-2x2和抛物线上一点P(1,-2).
已知抛物线y=-2x2和抛物线上一点P(1,-2).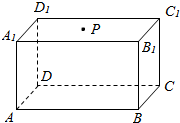 如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l
如图,P为长方体ABCD-A1B1C1D1的上底面A1B1C1D1内的一点,过直线BC与点P的平面记为α,若α∩平面A1B1C1D1=l