题目内容
4.己知函数f(x)定义在(-1,1)上,对于任意的x,y∈(-1,1),有f(x)+f(y)=f($\frac{x+y}{1+xy}$),且当x<0时,f(x)>0;(1)证明函数f(x)是奇函数;
(2)证明函数f(x)在(-1,1)上是减函数;
(3)若函数f(x)=1n$\frac{1-x}{1+x}$,证明:f(x)+f(y)=f($\frac{x+y}{1+xy}$).
分析 (1)要判定函数f(x)在(-1,1)上的奇偶性,只需判定f(-x)与f(x)的关系,先令x=y=0求出f(0),然后令y=-x即可判定;
(2)根据函数单调性的定义进行判定单调性;
(3)先求定义域看其是否满足条件,然后验证函数是否满f(x)+f(y)=f($\frac{x+y}{1+xy}$)即可.
解答 (1)证明:∵f(0)+f(0)=f(0)⇒f(0)=0
∴f(-x)+f(x)=f(0)=0⇒f(-x)=-f(x)
∴f(x)在(-1,1)上是奇函数.
(2)证明:f(x)-f(y)=f($\frac{x-y}{1-xy}$),
当-1<x<y<1时,$\frac{x-y}{1-xy}$,由条件知f($\frac{x-y}{1-xy}$)>0,
即f(x)-f(y)>0,
∴f(x)在(-1,1)上是减函数;
(3)解:由$\frac{1-x}{1+x}$>0可得-1<x<1,即其定义域为(-1,1)
又f(x)+f(y)=1n$\frac{1-x}{1+x}$+ln$\frac{1-y}{1+y}$=1n($\frac{1-x}{1+x}$•$\frac{1-y}{1+y}$)=f($\frac{x+y}{1+xy}$).
点评 本题主要考查抽象函数的奇偶性与单调性性,属于中档题,函数的奇偶性是函数在定义域上的“整体”性质,单调性是函数的“局部”性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数y=2x与y=log2x的图象( )
| A. | 关于x轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线y=x对称 | D. | 关于直线y=-x对称 |
19.已知f′(x)是定义在R上的奇函数f(x)的导数,且2f(x)+xf′(x)>x2,则函数f(x)的零点的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 1个或2个 |
16.第三象限的角的集合可表示为( )
| A. | {α|90°<α<180°} | B. | {α|180°<α<270°} | ||
| C. | {α|90°+k•360°<α<180°+k•360°,k∈Z} | D. | {α|180°+k•360°<α<270°+k•360°,k∈Z} |
 ,各项
,各项 ,公比为
,公比为 .(1)设
.(1)设 ,求证:
,求证: 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项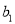 及公差
及公差 ;
; 的取值范围.
的取值范围.