题目内容
9.生产一种机器的固定收入为每年5万元,每生产1百台,需另增加投入6万元,已知客户群对比产品的年需求量不低于1百台而不超过5百台,年销售收入函数为R(x)=11x+$\frac{20}{x}$(1≤x≤5)(单位:万元),其中x是产品的年销售量(单位:百台),且每年生产的产品全部售出.(1)把年利润y表示为年销售量x的函数;
(2)当年销售量是多少时,工厂所得的年利润最低?最低是多少?
分析 (1)利用“利润=销售收入-成本”列式即可;
(2)利用基本不等式5x+$\frac{20}{x}$≥2$\sqrt{5x•\frac{20}{x}}$当且仅当5x=$\frac{20}{x}$即x=2时取等号,进而可得结论.
解答 解:(1)依题意,y=11x+$\frac{20}{x}$-(5+6x)=5x+$\frac{20}{x}$-5(1≤x≤5)(单位:万元);
(2)∵5x+$\frac{20}{x}$≥2$\sqrt{5x•\frac{20}{x}}$=20,当且仅当5x=$\frac{20}{x}$即x=2时取等号,
∴当年销售量是2百台时,工厂所得的年利润最低,最低是20万元.
点评 本题考查函数在生产生活中的实际应用,解题时要认真审题,注意分析题设条件中的数量关系,合理地进行等价转化,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
17.在锐角△ABC中,已知AB=2,∠B=2∠C,则AC的取值范围是( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{2}$) | C. | (2$\sqrt{2}$,4) | D. | (2,2$\sqrt{3}$) |
18.已知全集U={x||x|≤2},A={x|x2+x-2≤0},则∁UA=( )
| A. | {x|1≤x≤2} | B. | {x|1<x≤2} | C. | {x|-1≤x≤2} | D. | {x|-1<x≤2} |
 中,
中,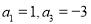 ,则
,则 ____________.
____________.