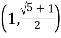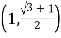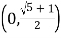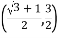题目内容
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销,定价为1000元/件.
(1)设日销售40个零件的概率为![]() ,记5天中恰有2天销售40个零件的概率为
,记5天中恰有2天销售40个零件的概率为![]() ,写出
,写出![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 极大值点
极大值点![]() .
.
(2)试销结束后统计得到该4S店这30内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 |
其中,有两个数据未给出.试销结束后,这款零件正式上市,每件的定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有55件,批发价为550元/件;小箱每箱有40件,批发价为600元/件,以这30天统计的各日销售量的频率作为试销后各日销售量发生的概率.该4S店决定每天批发两箱,若同时批发大箱和小箱,则先销售小箱内的零件,同时根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店,假设日销售量为80件的概率为![]() ,其中
,其中![]() 为(1)中
为(1)中![]() 的极大值点.
的极大值点.
(i)设该4S店批发两大箱,当天这款零件的利润为随机变量![]() ;批发两小箱,当天这款零件的利润为随机变量
;批发两小箱,当天这款零件的利润为随机变量![]() ,求
,求![]() 和
和![]() ;
;
(ii)以日利润的数学期望作为决策依据,该4S店每天应该按什么方案批发零件?
【答案】(1)![]() ,
,![]() .(2)(i)
.(2)(i)![]() =2.526万元,
=2.526万元,![]() =2.28万元;(ii)两大箱
=2.28万元;(ii)两大箱
【解析】
(1)利用二项式定理求出![]() 关于
关于![]() 函数,对函数
函数,对函数![]() 进行求导,利用导数判断函数
进行求导,利用导数判断函数![]() 的单调性求出极大值点
的单调性求出极大值点![]() 即可;
即可;
(2)(i)利用(1)中![]() 的值,分别求出日销售量为40件,60件,80件,100件的概率,然后求出批发为两大箱时所对应的利润,代入数学期望公式求出
的值,分别求出日销售量为40件,60件,80件,100件的概率,然后求出批发为两大箱时所对应的利润,代入数学期望公式求出![]() ;求出批发为两小箱时所对应的利润,代入数学期望公式求出
;求出批发为两小箱时所对应的利润,代入数学期望公式求出![]() 即可;
即可;
(ii)设当该4S店批发一大箱和一小箱时,成本为54250元,当天这款零件的利润为随机变量![]() ,分别求出日销售量分别为40件,60件,80件,100件的利润,代入数学期望公式求出
,分别求出日销售量分别为40件,60件,80件,100件的利润,代入数学期望公式求出![]() ,比较
,比较![]() 、
、![]() 和
和![]() 的大小即可.
的大小即可.
(1)由题意可得,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 有极大值,故
有极大值,故![]() .
.
(2)由题意可知,日销售量为80件的概率为![]() ,
,
日销售量为60件的概率为![]() ,日销售量为40件的概率为
,日销售量为40件的概率为![]() ,
,
所以日销售量为100的概率为![]() .
.
(i)批发两大箱,则批发成本为60500元,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件时,利润为![]() (万元);
(万元);
当日销售量为100件时,利润为![]() (万元),
(万元),
所以![]() (万元).
(万元).
若批发两小箱,则批发成本为48000元,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件或100件时,利润为![]() (万元),
(万元),
所以![]() (万元);
(万元);
(ii)当该4S店批发一大箱和一小箱时,成本为54250元,当天这款零件的利润为随机变量![]() ,
,
当日销售量为40件时,利润为![]() (万元);
(万元);
当日销售量为60件时,利润为![]() (万元);
(万元);
当日销售量为80件时,利润为![]() (万元);
(万元);
当日销售量为100件时,利润为![]() (万元);
(万元);
所以![]() (万元),
(万元),
所以![]() ,故该4S店每天应该批发两大箱.
,故该4S店每天应该批发两大箱.

【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: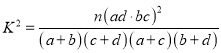 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |