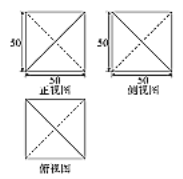
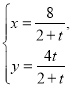题目内容
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() ,则双曲线的渐近线斜率的平方的取值范围是( )
,则双曲线的渐近线斜率的平方的取值范围是( )
A.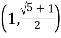 B.
B.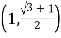
C.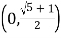 D.
D.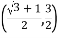
【答案】A
【解析】
根据题意,先求得直线![]() 的方程,由在线段
的方程,由在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() 可得线段
可得线段![]() 与以
与以![]() 为直径的圆相交,即可求得
为直径的圆相交,即可求得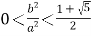 ;再根据
;再根据![]() 即可得双曲线的渐近线斜率的平方的取值范围.
即可得双曲线的渐近线斜率的平方的取值范围.
双曲线![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,
为虚轴的一个端点,
不妨设![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
因为在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() ,
,
所以线段![]() 与以
与以![]() 为直径的圆相交,即
为直径的圆相交,即 ,
,
化简可得![]() ,
,
双曲线中满足![]() ,代入上述不等式可得
,代入上述不等式可得![]() ,
,
则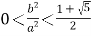 ,
,
由在线段![]() (不含端点)上存在两点
(不含端点)上存在两点![]() ,
,![]() ,使得
,使得![]() 可知
可知![]() ,
,
所以 ,即双曲线的渐近线斜率的平方的取值范围为
,即双曲线的渐近线斜率的平方的取值范围为 ,
,
故选:A.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
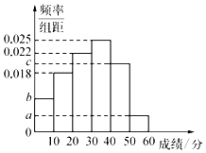
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: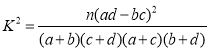 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销,定价为1000元/件.
(1)设日销售40个零件的概率为![]() ,记5天中恰有2天销售40个零件的概率为
,记5天中恰有2天销售40个零件的概率为![]() ,写出
,写出![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 极大值点
极大值点![]() .
.
(2)试销结束后统计得到该4S店这30内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 |
其中,有两个数据未给出.试销结束后,这款零件正式上市,每件的定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有55件,批发价为550元/件;小箱每箱有40件,批发价为600元/件,以这30天统计的各日销售量的频率作为试销后各日销售量发生的概率.该4S店决定每天批发两箱,若同时批发大箱和小箱,则先销售小箱内的零件,同时根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店,假设日销售量为80件的概率为![]() ,其中
,其中![]() 为(1)中
为(1)中![]() 的极大值点.
的极大值点.
(i)设该4S店批发两大箱,当天这款零件的利润为随机变量![]() ;批发两小箱,当天这款零件的利润为随机变量
;批发两小箱,当天这款零件的利润为随机变量![]() ,求
,求![]() 和
和![]() ;
;
(ii)以日利润的数学期望作为决策依据,该4S店每天应该按什么方案批发零件?