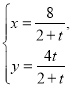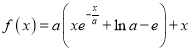题目内容
【题目】若a,b∈R.则“关于x的方程![]() 有两个不等实数根”是“a >|b|+1”的( )
有两个不等实数根”是“a >|b|+1”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【解析】
若已知关于![]() 的方程
的方程![]() 有两个不等实数根,由根的判别式得出
有两个不等实数根,由根的判别式得出![]() ,由于
,由于![]() ,
,![]() ,可取
,可取![]() ,进行验算即可判断不能推出
,进行验算即可判断不能推出![]() ,反之已知
,反之已知![]() ,则
,则![]() ,利用
,利用![]() ,可得出
,可得出![]() ,则
,则![]() ,可知能推出方程
,可知能推出方程![]() 有两个不等实数根,最后根据充分条件和必要条件的定义进行判断即可得出答案.
有两个不等实数根,最后根据充分条件和必要条件的定义进行判断即可得出答案.
解:由题可知,![]() ,
,![]() ,
,
若已知关于![]() 的方程
的方程![]() 有两个不等实数根,
有两个不等实数根,
则![]() ,即
,即![]() ,
,
取![]() 时满足
时满足![]() ,即
,即![]() ,则方程
,则方程![]() 有两个不等实数根,
有两个不等实数根,
但此时![]() ,故充分条件不成立;
,故充分条件不成立;
反之,若已知![]() ,即
,即![]() ,则
,则![]() ,
,
由于![]() ,即
,即![]() ,
,
所以![]() ,则有
,则有![]() ,即
,即![]() ,则方程
,则方程![]() 有两个不等实数根,
有两个不等实数根,
故必要条件成立;
所以“关于![]() 的方程
的方程![]() 有两个不等实数根”是“
有两个不等实数根”是“![]() ”的必要不充分条件.
”的必要不充分条件.
故选:B.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销,定价为1000元/件.
(1)设日销售40个零件的概率为![]() ,记5天中恰有2天销售40个零件的概率为
,记5天中恰有2天销售40个零件的概率为![]() ,写出
,写出![]() 关于
关于![]() 的函数关系式,并求
的函数关系式,并求![]() 极大值点
极大值点![]() .
.
(2)试销结束后统计得到该4S店这30内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 |
其中,有两个数据未给出.试销结束后,这款零件正式上市,每件的定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有55件,批发价为550元/件;小箱每箱有40件,批发价为600元/件,以这30天统计的各日销售量的频率作为试销后各日销售量发生的概率.该4S店决定每天批发两箱,若同时批发大箱和小箱,则先销售小箱内的零件,同时根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店,假设日销售量为80件的概率为![]() ,其中
,其中![]() 为(1)中
为(1)中![]() 的极大值点.
的极大值点.
(i)设该4S店批发两大箱,当天这款零件的利润为随机变量![]() ;批发两小箱,当天这款零件的利润为随机变量
;批发两小箱,当天这款零件的利润为随机变量![]() ,求
,求![]() 和
和![]() ;
;
(ii)以日利润的数学期望作为决策依据,该4S店每天应该按什么方案批发零件?