题目内容
半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.则四边形OACB的面积最大值是 。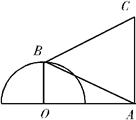

2+
设∠AOB=α,在△AOB中,由余弦定理得
AB2=12+22-2×1×2cosα=5-4cosα,于是,四边形OACB的面积为
S=S△AOB+S△ABC=OA·OBsinα+AB2
=×2×1×sinα+(5-4cosα)
=sinα-cosα+
=2sin(α-)+
∵0<α<π,
∴当α-=,α=π,即∠AOB=时,四边形OACB面积最大为2+.
AB2=12+22-2×1×2cosα=5-4cosα,于是,四边形OACB的面积为
S=S△AOB+S△ABC=OA·OBsinα+AB2
=×2×1×sinα+(5-4cosα)
=sinα-cosα+
=2sin(α-)+
∵0<α<π,
∴当α-=,α=π,即∠AOB=时,四边形OACB面积最大为2+.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为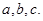 已知
已知 且
且 .
. 时,求
时,求 的值;
的值; 为锐角,求
为锐角,求 的取值范围.
的取值范围. 是等边三角形,
是等边三角形, 是等腰直角三角形,
是等腰直角三角形,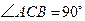 ,
,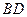 交
交 于
于 ,
, .
. 的值;
的值; .
. 
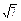 ,且4sin2
,且4sin2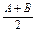 -cos2C=
-cos2C=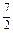 .
. ,B=60
,B=60