题目内容
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() .
.
(1)求![]() 的最小正周期及
的最小正周期及![]() 图象的对称轴方程;
图象的对称轴方程;
(2)若先将![]() 的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移
的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 内的所有零点之和.
内的所有零点之和.
【答案】(1)最小正周期为![]() ,对称轴方程为
,对称轴方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)结合向量的数量积的坐标运算,化简求得![]() ,再利用三角函数的图象与性质,即可求解;
,再利用三角函数的图象与性质,即可求解;
(2)根据三角函数的图象变换,求得![]() ,结合函数的零点的概念和正弦函数的图象的性质,即可求解.
,结合函数的零点的概念和正弦函数的图象的性质,即可求解.
(1)由题意,向量![]() ,
,![]() ,
,
所以![]()
![]()
![]()
![]()
![]() .
.
可得![]() ,即函数的最小正周期为
,即函数的最小正周期为![]() ,
,
令![]() ,解得
,解得![]()
所以函数![]() 的最小正周期为
的最小正周期为![]() ,对称轴方程为
,对称轴方程为![]() .
.
(2)由(1)知![]() ,
,
将![]() 的图象上每个点横坐标变为原来的2倍,可得
的图象上每个点横坐标变为原来的2倍,可得![]() ,
,
然后将![]() 向左平移
向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() ,
,
令![]() ,即
,即![]() ,
,
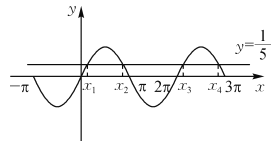
由图可知,![]() 在
在![]() 上有4个零点:
上有4个零点:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
根据对称性有![]() ,
,![]() ,
,
所以所有零点和为![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目