题目内容
一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是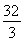 π,那么这个三棱柱的体积是________.
π,那么这个三棱柱的体积是________.
48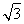
【解析】因为球的体积为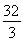 π,柱体的高为2r=4,又正三棱柱的底面三角形内切圆半径与球半径相等,r=2,所以底面边长a=4
π,柱体的高为2r=4,又正三棱柱的底面三角形内切圆半径与球半径相等,r=2,所以底面边长a=4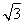 ,所以V柱=
,所以V柱=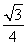 ×(4
×(4 )2×4=48
)2×4=48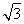 .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
题目内容
一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是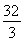 π,那么这个三棱柱的体积是________.
π,那么这个三棱柱的体积是________.
48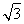
【解析】因为球的体积为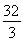 π,柱体的高为2r=4,又正三棱柱的底面三角形内切圆半径与球半径相等,r=2,所以底面边长a=4
π,柱体的高为2r=4,又正三棱柱的底面三角形内切圆半径与球半径相等,r=2,所以底面边长a=4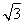 ,所以V柱=
,所以V柱=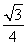 ×(4
×(4 )2×4=48
)2×4=48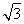 .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案