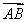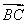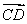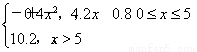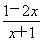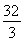题目内容
已知不等式(2+x)(3-x)≥0的解集为A,函数f(x)=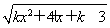 (k<0)的定义域为B.
(k<0)的定义域为B.
(1)求集合A;
(2)若集合B中仅有一个元素,试求实数k的值;
(3)若B?A,试求实数k的取值范围.
(1)A=[-2,3](2)k=-4(3)-4≤k≤-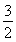
【解析】(1)由(2+x)(3-x)≥0,得(2+x)(x-3)≤0,解得-2≤x≤3,故A=[-2,3].
(2)记g(x)=kx2+4x+k+3,则g(x)≥0在R上有且仅有一解,而k<0,所以Δ=0.由k<0与16-4k(k+3)=0,解得k=-4.
(3)记g(x)=kx2+4x+k+3,首先g(x)≥0在R上有解,而k<0,所以Δ=16-4k(k+3)≥0,解之得-4≤k<0.①设g(x)=0的两个根为x1,x2(x1<x2),则B=[x1,x2].
由BA,得 即
即 ②由①与②,解得-4≤k≤-
②由①与②,解得-4≤k≤-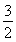 .
.

练习册系列答案
相关题目