题目内容
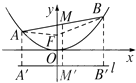
已知P为抛物线C：y2=4x上的一点，F为抛物线C的焦点，其准线与x轴交于点N，直线NP与抛物线交于另一点Q，且|PF|=3|QF|，则点P坐标为______．
∵y2=4x，
∴焦点坐标F（1，0），准线方程x=-1．
过P，Q分别作准线的射影分别为A，B，
则由抛物线的定义可知：|PA|=|PF|，|QF|=|BQ|，
∵|PF|=3|QF|，
∴|AP|=3|QB|，
即|BN|=3|AN|，
∴P，Q的纵坐标满足yP=3yQ，
设P（
，y），y≠0，
则Q（
，
），
则N（-1，0），
∵N，Q，P三点共线，
∴
=
，
解得y2=12，
∴y=±2
，
此时x=
=
=3，
即点P坐标为（3，±2
），
故答案为：（3，±2
）
∴焦点坐标F（1，0），准线方程x=-1．
过P，Q分别作准线的射影分别为A，B，
则由抛物线的定义可知：|PA|=|PF|，|QF|=|BQ|，
∵|PF|=3|QF|，
∴|AP|=3|QB|，
即|BN|=3|AN|，
∴P，Q的纵坐标满足yP=3yQ，
设P（
| y2 |
| 4 |
则Q（
| y2 |
| 36 |
| y |
| 3 |
则N（-1，0），
∵N，Q，P三点共线，
∴
| y | ||
|
| ||
|
解得y2=12，
∴y=±2
| 3 |
此时x=
| y2 |
| 4 |
| 12 |
| 4 |
即点P坐标为（3，±2
| 3 |
故答案为：（3，±2
| 3 |
练习册系列答案
相关题目
