题目内容
(本题满分12分)
已知数列{an}的前n项和为Sn,点(n,)在直线y=x+上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
已知数列{an}的前n项和为Sn,点(n,)在直线y=x+上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),b3=11,且其前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn=,数列{cn}的前n项和为Tn,求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.
解:(1)由已知得=n+,∴Sn=n2+n.
当n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=n+5;
当n=1时,a1=S1=6也符合上式.∴an=n+5.
由bn+2-2bn+1+bn=0(n∈N*)知{bn}是等差数列,
由{bn}的前9项和为153,可得=9b5=153,
得b5=17,又b3=11,∴{bn}的公差d==3,b3=b1+2d,
∴b1=5,∴bn=3n+2.
(2)cn==(-),
∴Tn=(1-+-+…+-)
=(1-).∵n增大,Tn增大,∴{Tn}是递增数列.∴Tn≥T1=.
Tn>对一切n∈N*都成立,只要T1=>,
∴k<19,则kmax=18.
略

练习册系列答案
相关题目
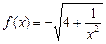 ,点
,点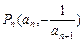 在曲线
在曲线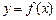 上
上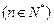 且
且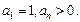 (Ⅰ)求证:数列
(Ⅰ)求证:数列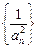 为等差数列,并求数列
为等差数列,并求数列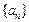 的通项公式;
的通项公式;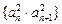 的前n项和为
的前n项和为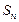 ,若对于任意的
,若对于任意的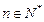 ,存在正整数t,使得
,存在正整数t,使得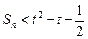 恒成立,求最小正整数t的值
恒成立,求最小正整数t的值 ,且有an-1-an-4an-1an="0,"
,且有an-1-an-4an-1an="0," 
 为等差数列;
为等差数列; 中的项?如果是, 是第几项;如果不是,请说明理由.
中的项?如果是, 是第几项;如果不是,请说明理由.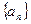 满足
满足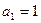 ,
,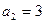 ,
,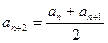 ,
,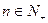
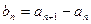 ,证明:
,证明: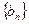 是等比数列;
是等比数列; 是首项
是首项 的等比数列,其前
的等比数列,其前 项和
项和 中
中 ,
, ,
, 成等差数列,
成等差数列, ,若
,若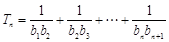 ,求证:
,求证: .
. 中,
中,
 ,
, ,则使前
,则使前 项和
项和 成立的最大自然数
成立的最大自然数







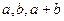 成等差数列,
成等差数列,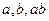 成等比数列,则通项为
成等比数列,则通项为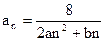 的数列
的数列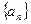 的前n项和为
的前n项和为  中,
中, ,则
,则 的值为
的值为 