题目内容

19．已知10α=${2}^{-\frac{1}{2}}$，10β=${16}^{\frac{1}{3}}$，则${10}^{2α-\frac{3}{4}β}$=$\frac{1}{4}$．

分析 化简102α=$\frac{1}{2}$，$1{0}^{\frac{3}{4}β}$=2，从而解得．

解答 解：102α=（10α）2=2-1=$\frac{1}{2}$，
$1{0}^{\frac{3}{4}β}$=$（1{0}^{β}）^{\frac{3}{4}}$=$（1{6}^{\frac{1}{3}}）^{\frac{3}{4}}$=$1{6}^{\frac{1}{4}}$=2，
故${10}^{2α-\frac{3}{4}β}$=$\frac{1}{2}$÷2=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．

点评 本题考查了有理指数幂的化简与应用．

练习册系列答案
相关题目
9．“x2+y2≤1”是“|x|+|y|≤$\sqrt{2}$”成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充分且必要条件D．既不充分又不必要条件
10．已知函数f（x）=x2，写出函数y=f（x2-2x-3））的单调区间．
7．化简：
（1）$\sqrt{7+4\sqrt{3}}$-$\sqrt{5-2\sqrt{6}}$=2+$\sqrt{2}$；
（2）当a≥1时，$\sqrt{a+2\sqrt{a-1}}$+$\sqrt{a-2\sqrt{a-1}}$=$\left\{\begin{array}{l}{2\sqrt{a-1}，a≥5}\\{2，1≤a＜5}\end{array}\right.$．
14．设a=（$\frac{2}{5}$）${\;}^{\frac{2}{5}}$，b=（$\frac{2}{5}$）${\;}^{\frac{3}{5}}$，c=log${\;}_{\frac{1}{4}}$3，则a，b，c的大小关系是（　　）
A．a＞c＞bB．a＞b＞cC．c＞a＞bD．c＞b＞a
4．已知函数f（x）=x2+ax+1，若存在x0，使|f（x0）|$≤\frac{1}{4}$，|f（x0+1）|≤$\frac{1}{4}$同时成立，则a的取值范围是（　　）
A．[4，6]B．[-$\sqrt{6}$，-2]C．[2，$\sqrt{6}$]D．[-$\sqrt{6}$，-2]∪[2，$\sqrt{6}$]
11．已知数列{an}的通项公式an=2n-6（n∈N*）．
（1）求证：{an}是等差数列；
（2）若a2、a5分别是等比数列{bn}的第1项和第2项，求数列{bn}的通项公式bn．
8．函数f（x）=Asin（wx+φ）（A＞0，w＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（$\frac{3π}{2}$）的值是（　　）
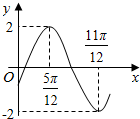
A．-1B．1C．-$\sqrt{3}$D．$\sqrt{3}$
5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，m2），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则 m的值为（　　）
A．2或-1B．-2或1C．±2D．±1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网