题目内容
20.已知函数f(x)=$\sqrt{3}$sinxcosx-cos(2x+$\frac{π}{3}$)-cos2x,求函数的最小正周期及最值,单增区间.分析 由三角函数中的恒等变换应用化简可得函数解析式为f(x)=2sin(2x-$\frac{π}{6}$)$-\frac{1}{2}$,由三角函数的周期性及其求法可求函数的最小正周期,由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,可得-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,可得f(x)的单调增区间,由正弦函数的图象和性质即可求得最值.
解答 解:∵f(x)=$\sqrt{3}$sinxcosx-cos(2x+$\frac{π}{3}$)-cos2x
=$\frac{\sqrt{3}}{2}$sin2x-[$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x]-$\frac{1+cos2x}{2}$
=$\sqrt{3}$sin2x-cos2x-$\frac{1}{2}$
=2sin(2x-$\frac{π}{6}$)$-\frac{1}{2}$,
∴函数的最小正周期T=$\frac{2π}{2}=π$.
∴由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,可得-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,可得f(x)的单调增区间为[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z),
∴函数的最大值为$\frac{3}{2}$,最小值为-$\frac{5}{2}$.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质的应用,属于基本知识的考查.

练习册系列答案
相关题目
12.设直线l1:y=$\sqrt{3}$x-1,l2:y=$\frac{\sqrt{3}}{3}$x+3,则l1到l2的角是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
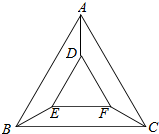 如图,用五种不同的颜色给图中的A,B,C,D,E,F六个不同的点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有1920种.
如图,用五种不同的颜色给图中的A,B,C,D,E,F六个不同的点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同的颜色,则不同的涂色方法共有1920种.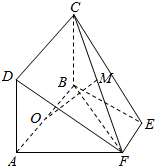 如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.
如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.