题目内容
【题目】已知几何体A﹣BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. 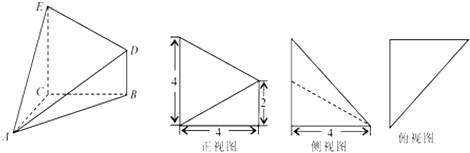
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
【答案】
(1)解:∵∠ACE,∠ACB都是直角,∴AC⊥BC,AC⊥CE,CB∩CE=C,CB平面BCED,CE平面BCED;
∴AC⊥平面BCED.
∴V= ![]() .
.
(2)解:取CE中点F,连接BF,则BF∥DE,则∠ABF即异面直线DE与AB所成的角,连接AF.
在△ABF中,AB=4 ![]() ,BF=
,BF= ![]() ,AF=
,AF= ![]() ;
;
∴由余弦定理得:cos∠ABF= ![]() ;
;
异面直线DE与AB所成角的余弦值是 ![]() .
.
(3)解:过C作CG⊥DE,交DE于G,连接AG,∵AC⊥平面BCED,ED平面BCED,∴AC⊥ED;
∴ED⊥平面ACG,AG平面ACG,∴ED⊥AG,∴∠AGC是二面角A﹣ED﹣B的平面角;
在Rt△ACG中,AC=4,CG= ![]() ,∠ACG=90°;
,∠ACG=90°;
∴tan∠AGC= ![]() ,sin
,sin ![]() .
.
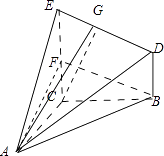
【解析】(1)通过已知条件可知,AC⊥底面BCED,再求出梯形BCED的面积,根据三棱锥的体积公式即可求出体积.(2)先找到异面直线所成的角,可过B作DE的平行线,则角ABF便是异面直线所成的角,根据条件求出即可.(3)先找出二面角的平面角,过C作CG⊥ED,并交ED于G,连接AG,则∠AGC即是所找的二面角的平面角,根据条件求出即可.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】有一个容量为60的样本(60名学生的数学考试成绩),分组情况如表:
分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
频数 | 3 | 6 | 12 | ||
频率 | 0.3 |
(1)填出表中所剩的空格;
(2)画出频率分布直方图.