题目内容
已知命题p:“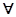 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“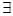 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
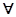 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“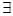 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )A.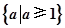 | B.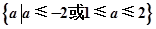 |
C.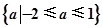 | D.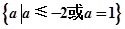 |
D
试题分析:若
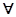 x∈[1,2],x2-a≥0,则
x∈[1,2],x2-a≥0,则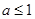 ;若
;若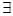 x∈R使x2+2ax+2-a=0,则
x∈R使x2+2ax+2-a=0,则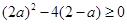 ,解得
,解得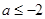 或
或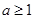 ,若命题“p且q”是真命题,则实数a满足
,若命题“p且q”是真命题,则实数a满足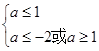 ,
,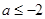 或
或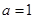 ,所以实数a的取值范围是
,所以实数a的取值范围是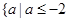 或
或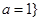 .
.
练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
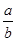 =-1
=-1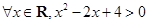 ”的否定为 .
”的否定为 .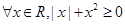 ”的否定是( )
”的否定是( )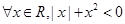
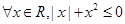
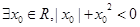
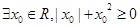
 ,则“
,则“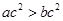 ”是“
”是“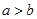 ”成立的充分不必要条件;
”成立的充分不必要条件;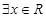 使得
使得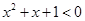 ”的否定是“
”的否定是“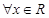 均有
均有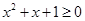 ”;
”;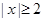 ,则
,则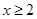 或
或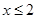 ”的否命题是“若
”的否命题是“若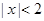 ,则
,则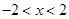 ”;
”;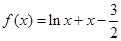 在区间
在区间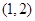 上有且仅有一个零点.
上有且仅有一个零点.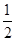 ,
,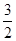 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围. p1)∧(
p1)∧(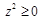 , 则z是实数
, 则z是实数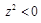 , 则z是虚数
, 则z是虚数