题目内容
下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若 ,则“
,则“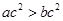 ”是“
”是“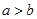 ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“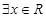 使得
使得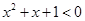 ”的否定是“
”的否定是“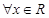 均有
均有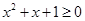 ”;
”;
③命题“若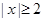 ,则
,则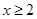 或
或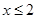 ”的否命题是“若
”的否命题是“若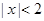 ,则
,则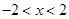 ”;
”;
④函数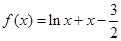 在区间
在区间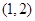 上有且仅有一个零点.
上有且仅有一个零点.
①若
 ,则“
,则“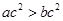 ”是“
”是“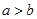 ”成立的充分不必要条件;
”成立的充分不必要条件;②命题“
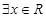 使得
使得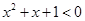 ”的否定是“
”的否定是“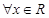 均有
均有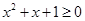 ”;
”;③命题“若
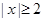 ,则
,则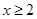 或
或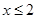 ”的否命题是“若
”的否命题是“若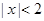 ,则
,则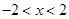 ”;
”;④函数
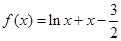 在区间
在区间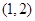 上有且仅有一个零点.
上有且仅有一个零点.①②③④
试题分析:对于①,当
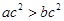 时,说明
时,说明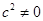 且
且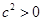 ,于得两边同乘
,于得两边同乘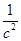 可得
可得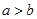 ,反过来当
,反过来当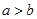 时,不一定有
时,不一定有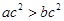 ,如
,如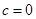 时,
时,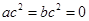 ,所以“
,所以“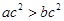 ”是“
”是“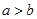 ”成立的充分不必要条件;对于②,根据特称命题的否定是全称命题可知:命题“
”成立的充分不必要条件;对于②,根据特称命题的否定是全称命题可知:命题“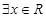 使得
使得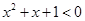 ”的否定是“
”的否定是“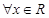 均有
均有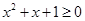 ”;对于③,根据否命题的定义:原命题为若
”;对于③,根据否命题的定义:原命题为若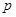 则
则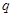 ,则它的否命题为若
,则它的否命题为若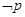 则
则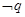 ,所以:命题“若
,所以:命题“若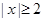 ,则
,则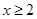 或
或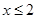 ”的否命题是“若
”的否命题是“若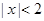 ,则
,则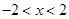 ”;对于④,因为函数
”;对于④,因为函数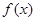 的定义域为
的定义域为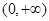 ,所以
,所以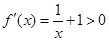 ,所以函数
,所以函数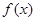 在
在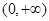 单调递增,又
单调递增,又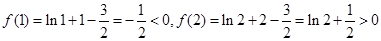 ,根据零点存在定理可知
,根据零点存在定理可知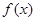 在区间
在区间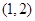 至少存在一个零点,而
至少存在一个零点,而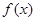 在
在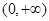 单调递增,所以
单调递增,所以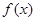 在区间
在区间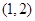 有且仅有一个零点.
有且仅有一个零点.
练习册系列答案
相关题目
 的否定是( )
的否定是( )



 ( )
( )



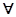 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“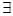 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )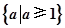
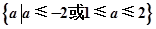
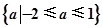
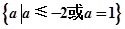
 )x<(
)x<( )x;
)x; x>
x> x;
x;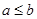 ,则
,则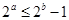 ”的否命题;
”的否命题;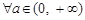 ,函数
,函数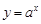 在定义域内单调递增”的否定;
在定义域内单调递增”的否定;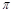 是函数
是函数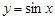 的一个周期”或“
的一个周期”或“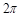 是函数
是函数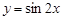 的一个周期”;
的一个周期”;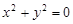 ”是“
”是“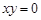 ”的必要条件.
”的必要条件.