题目内容
(12分)已知 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足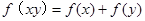 ,
, 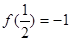
(1)求证: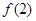 =1 (2) 求不等式
=1 (2) 求不等式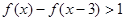 的解集.
的解集.
(1)见解析;(2){x/3<x<6}。
解析试题分析:(1)由题意得f(1)=f(1×1)=f(1)+f(1)=2f(1) ∴f(1)=0,进一步得到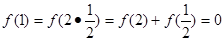 .
.
(2)不等式化为f(x)>f(x-3)+1
∵f(2)=1
∴f(x)>f(x-3)+f(2)=f(2x-6)
∵f(x)是(0,+∞)上的增函数
∴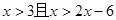 解得{x/3<x<6}
解得{x/3<x<6}
(1)【证明】 由题意得f(1)=f(1×1)=f(1)+f(1)=2f(1) ∴f(1)=0 3分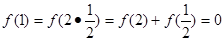 ∴
∴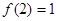 。。。6分
。。。6分
(2)【解】 不等式化为f(x)>f(x-3)+1
∵f(2)=1
∴f(x)>f(x-3)+f(2)=f(2x-6)
∵f(x)是(0,+∞)上的增函数
∴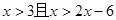 解得{x/3<x<6} 。。。。12分
解得{x/3<x<6} 。。。。12分
考点:本题主要是考查抽象函数单调性的运用。
点评:解决该试题的关键是利用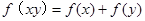 和
和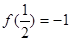 得到f(2)=1,进而变形得到不等式的解集。
得到f(2)=1,进而变形得到不等式的解集。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
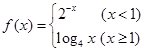 ,
,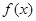 的图像;
的图像;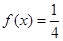 的
的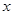 的取值.
的取值.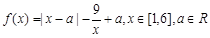 。
。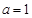 ,试判断并证明
,试判断并证明 的单调性;
的单调性;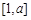 上单调,且存在
上单调,且存在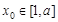 使
使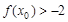 成立,求
成立,求 的取值范围;
的取值范围;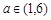 时,求函数
时,求函数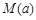 。
。 的一系列对应值如下表:
的一系列对应值如下表: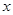







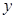



 的解析式;
的解析式; 周期为
周期为 ,求
,求 在区间
在区间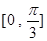 上的最大、最小值及对应的
上的最大、最小值及对应的 是定义在
是定义在 上的单调增函数,满足
上的单调增函数,满足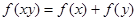 ,
,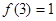 ,
,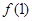 ;
;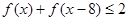 ,求
,求 的取值范围。
的取值范围。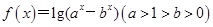 .
. 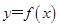 的定义域;
的定义域;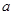 ,b满足什么条件时,
,b满足什么条件时,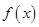 在
在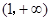 上恒取正值.
上恒取正值.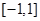 上的奇函数
上的奇函数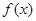 ,当
,当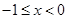 时,
时,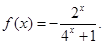
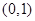 上的单调性,并给予证明;
上的单调性,并给予证明;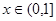 时,关于
时,关于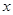 的方程
的方程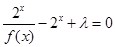 有解,试求实数
有解,试求实数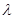 的取值范围.
的取值范围.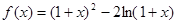 .
.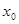 ,使不等式
,使不等式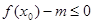 成立,求实数
成立,求实数 的最小值;
的最小值;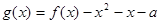 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 取值范围.
取值范围. (
(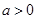 ),
),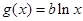 .
.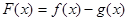 ,讨论
,讨论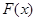 的单调性;
的单调性; 的不等式
的不等式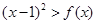 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数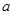 的取值范围;
的取值范围; 与
与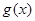 定义域上的任意实数
定义域上的任意实数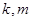 ,使得
,使得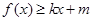 和
和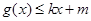 都成立,则称直线
都成立,则称直线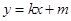 为函数
为函数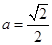 ,
,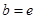 ,试探究
,试探究