题目内容
本题12分)
已知函数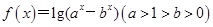 .
.
(1)求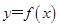 的定义域;
的定义域;
(2)在函数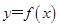 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当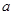 ,b满足什么条件时,
,b满足什么条件时,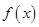 在
在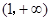 上恒取正值.
上恒取正值.
(1) (0,+∞).(2)函数y=f(x)的图象上不存在不同的两点使过两点的直线平行于x轴.
(3)当a≥b+1时, f(x)在(1,+∞)上恒取正值.
解析试题分析:(1)由对数函数的真数大于零求解.
(2)当函数在定义域上单调时,则不存在,当函数在定义域上不单调时,则存在,所以要证明函数是否单调,可用定义法,也可用导数法研究.
(3)由“f(x)在(1,+∞)上恒取正值”则需函数的最小值非负即可,由(2)可知是增函数,所以只要f(1)≥0即可.
解 :(1)由ax-bx>0,
得(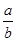 )x>1,且a>1>b>0,得
)x>1,且a>1>b>0,得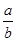 >1,
>1,
所以x>0,即f(x)的定义域为(0,+∞).
(2)任取x1>x2>0,a>1>b>0,则ax1>ax2>0,bx1<bx2,所以ax1-bx1>ax2-bx2>0,
即lg(ax1-bx1)>lg(ax2-bx2). 故f(x1)>f(x2).
所以f(x)在(0,+∞)上为增函数.
假设函数y=f(x)的图象上存在不同的两点A(x1,y1)、B(x2,y2),使直线平行于x轴, 则x1≠x2,y1=y2,这与f(x)是增函数矛盾.
故函数y=f(x)的图象上不存在不同的两点使过两点的直线平行于x轴.
(3)因为f(x)是增函数,
所以当x∈(1,+∞)时,f(x)>f(1). 这样只需f(1)=lg(a-b)≥0,
即当a≥b+1时, f(x)在(1,+∞)上恒取正值.
考点:本题主要考查函数的定义域,单调性及最值,这是常考常新的类型,在转化问题和灵活运用知识,方法方法要求较高.
点评:解决该试题的关键是利用导数的几何意义来表示切线的斜率,同时能利用对数的真数大于零得到定义域进而研究其性质。

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 .
. 的单调性;
的单调性; 的值;
的值; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 和
和 是函数
是函数 的两个极
的两个极 ,
, .(Ⅰ) 求
.(Ⅰ) 求 的取值范围;
的取值范围; ,求
,求 的最大值.
的最大值. .
. 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足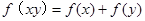 ,
, 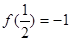
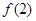 =1 (2) 求不等式
=1 (2) 求不等式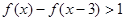 的解集.
的解集.  是奇函数:
是奇函数: 和
和 的值; (2)证明
的值; (2)证明 在区间
在区间 上的单调递减
上的单调递减 且不等式
且不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 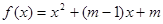 ,
,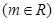
 是偶函数,求
是偶函数,求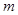 的值。
的值。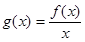 ,
,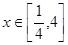 ,求
,求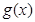 的最小值。
的最小值。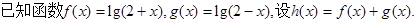
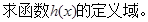
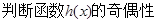 ,并说明理由.
,并说明理由.