题目内容
某市居民自来水收费标准如下，每户每月用水不超过4吨时，每吨为2元，当用水超过4吨时，超过部分每吨5元，若甲、乙两用户某月用水量比为5：3，且该月甲、乙两户共交水费19元，则甲、乙两户该月的水费分别为 ， ．
考点：函数模型的选择与应用
专题：计算题,函数的性质及应用
分析：设该月甲、乙两户的用水为5x吨，3x吨；利用分段函数求解．
解答：
解：设该月甲、乙两户的用水为5x吨，3x吨；
故当5x≤4，即x≤
；
5x×2+3x×2=19，
解得x=
，（舍去）；
当3x≤4＜5x，即
＜x≤
时，
5（5x-4）+4×2+3x×2=19，
即x=1，
故甲、乙两户该月的水费分别为：5+8=13，2×3=6；
故答案为：13元，6元．
故当5x≤4，即x≤
| 4 |
| 5 |
5x×2+3x×2=19，
解得x=
| 19 |
| 16 |
当3x≤4＜5x，即
| 4 |
| 5 |
| 4 |
| 3 |
5（5x-4）+4×2+3x×2=19，
即x=1，
故甲、乙两户该月的水费分别为：5+8=13，2×3=6；
故答案为：13元，6元．
点评：本题考查了分段函数在实际问题中的应用，属于中档题．
练习册系列答案
相关题目
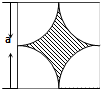如图所示，墙上挂有边长为a的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为| a |
| 2 |
A、
| ||
B、1-
| ||
C、1-
| ||
| D、与a的取值有关 |
已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（ ）
| A、若α⊥γ，β⊥γ，则α∥β |
| B、若m⊥α，n⊥α，则m∥n |
| C、若m∥α，n∥α，则m∥n |
| D、若m∥α，m∥β，则α∥β |