Question

一个几何体的正视图、侧视图都是腰长为

35

，底边长为4的等腰三角形，俯视图是边长为4的正方形，则其侧面积为

 

，体积为

 

．

Answer 1

考点：三垂线定理

专题：空间位置关系与距离

分析：依题意，可知底面边长为4的四棱锥P-ABCD为正四棱锥，利用已知的数据可知该锥体的斜高，进一步求得该锥体的高PO，从而可求得其侧面积与体积．

解答： 解：依题意，该几何体为一底面边长为4的正四棱锥P-ABCD，E、F分别为BC、AD的中点，PO⊥底面ABCD，

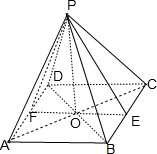
∵PE=

35

，OE=2，在Rt△POE中，PO=

( 35 )2-22

=

31

，
∴S_侧=4×（

1

2

BC×PE）=4×

1

2

×4×

35

=8

35

；
V_P-ABCD=

1

3

S_底面•PO=

1

3

×4²×

31

=

16

3

31

．
故答案为：8

35

；

16

3

31

．

点评：本题考查空间几何体的三视图，着重考查锥体的侧面积与体积的计算，考查作图能力与运算能力，是中档题．