题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
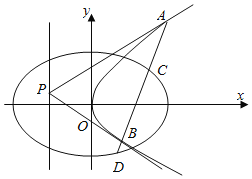
,焦距为![]() ,斜率为k的直线l与椭圆M有两个不同的交点A、B.
,斜率为k的直线l与椭圆M有两个不同的交点A、B.
(1)求椭圆M的方程;
(2)设P(﹣2,0),直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D,若C、D与点![]() 共线,求斜率k的值.
共线,求斜率k的值.
【答案】(1)![]() (2)2
(2)2
【解析】
(1)根据椭圆的离心率公式即可求得![]() 的值,即可求得
的值,即可求得![]() 的值,求得椭圆方程;
的值,求得椭圆方程;
(2)求得直线![]() 的方程,代入椭圆方程,即可根据韦达定理即可求得
的方程,代入椭圆方程,即可根据韦达定理即可求得![]() 点坐标,同理求得
点坐标,同理求得![]() 点坐标,即可求得
点坐标,即可求得![]() 与
与![]() 共线,根据向量的共线定理,即可求得直线
共线,根据向量的共线定理,即可求得直线![]() 的斜率.
的斜率.
解:(1)由题意可知:![]() ,则
,则![]() ,
,
椭圆的离心率![]() ,则
,则![]() ,
,
![]() ,
,
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立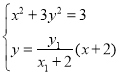 ,消去
,消去![]() 整理得
整理得
![]() ,
,
由![]() 代入上式得,整理得
代入上式得,整理得![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,
则![]() ,同理可得:
,同理可得:![]() ,
,
由![]() ,则
,则![]() ,
,![]() ,
,
由![]() 、
、![]() 与点
与点![]() 共线可得
共线可得![]() 与
与![]() 共线,
共线,
则![]() ,
,
整理得![]() ,
,
则直线![]() 的斜率
的斜率![]() ,
,
![]() 的值为2.
的值为2.

练习册系列答案
相关题目
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记![]() 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.