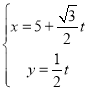题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的极值点;
的极值点;
(2)若函数![]() 在区间
在区间![]() 内无零点,求
内无零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() 或
或![]()
【解析】
(1)先求得函数的定义域,然后对函数求导,对![]() 分成
分成![]() 两类,讨论函数的单调区间,进而求得函数的极值点.(2)先求得函数
两类,讨论函数的单调区间,进而求得函数的极值点.(2)先求得函数![]() 的导数,对
的导数,对![]() 分成
分成![]() 三类,讨论函数的单调区间,结合零点的存在性定理,求得
三类,讨论函数的单调区间,结合零点的存在性定理,求得![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]()
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,![]() 无极值点;
无极值点;
当![]() 时,
时,![]() 时
时![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() 有极小值点
有极小值点![]() ,无极大值点.
,无极大值点.
(2)![]() ,
,![]()
![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,![]() ,所以无零点,满足条件;
,所以无零点,满足条件;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,![]() ,所以无零点,满足条件;
,所以无零点,满足条件;
当![]() 时,存在
时,存在![]() ,使得
,使得![]() ,
,
即![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 上一定存在零点,不符合条件.
上一定存在零点,不符合条件.
综上所述,![]() 或
或![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有6张奖券,其中一张印有900元字样,两张印有600元字样,三张印有300元字样,抽到奖券可获得相应奖金.6位客户每人随机抽取一张奖券(不放回),设6位客户中购买产品的客户人均所得奖金为![]() 元,求
元,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】未了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,将这100人的年龄数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,整理得到如图所示的频率分布直方图.
,整理得到如图所示的频率分布直方图.
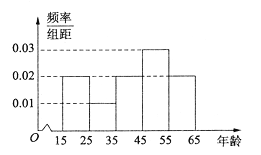
在这100人中不支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
不支持“延迟退休”的人数 | 15 | 5 | 15 | 23 | 17 |
(1)由频率分布直方图,估计这100人年龄的平均数;
(2)由频率分布直方图,若在年龄![]() ,
,![]() ,
,![]() 的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在
的三组内用分层抽样的方法抽取12人做问卷调查,求年龄在![]() 组内抽取的人数;
组内抽取的人数;
(3)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异?
\ | 45岁以下 | 45岁以上 | 总计 |
不支持 | |||
支持 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】为了调查某地区70岁以上老人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了100位70岁以上老人,结果如下:
男 | 女 | |
需要 | 18 | 5 |
不需要 | 32 | 45 |
(1)估计该地区70岁以上老人中,男、女需要志愿者提供帮助的比例各是多少?
(2)能否有![]() 的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关;
的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关;
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区70岁以上老人中,需要志愿者提供帮助的老人的比例?说明理由.
附:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,
,![]() .
.
【题目】新冠状病毒严重威胁着人们的身体健康,我国某医疗机构为了调查新冠状病毒对我国公民的感染程度,选了某小区的![]() 位居民调查结果统计如下:
位居民调查结果统计如下:
感染 | 不感染 | 合计 | |
年龄不大于 |
| ||
年龄大于 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为感染新冠状病与不同年龄有关?
的前提下认为感染新冠状病与不同年龄有关?
(3)已知在被调查的年龄大于![]() 岁的感染者中有
岁的感染者中有![]() 名女性,其中
名女性,其中![]() 位是女教师,现从这
位是女教师,现从这![]() 名女性中随机抽取
名女性中随机抽取![]() 人,求至多有
人,求至多有![]() 位教师的概率.
位教师的概率.
附: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|