题目内容
【题目】已知椭圆![]() 的中心在原点,焦点在坐标轴上,且经过
的中心在原点,焦点在坐标轴上,且经过![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)四边形![]() 的四个顶点都在椭圆
的四个顶点都在椭圆![]() 上,且对角线
上,且对角线![]() ,
,![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
【答案】(Ⅰ)标准方程![]() ,离心率
,离心率![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
(Ⅰ)先设椭圆方程,再由题意,列方程组求解即可;
(Ⅱ)先设![]() 的方程为
的方程为![]() ,联立直线与曲线方程,由根与系数关系,结合题意表示出
,联立直线与曲线方程,由根与系数关系,结合题意表示出![]() ,即可求出
,即可求出![]() 的关系式,进而由面积公式可求出结果.
的关系式,进而由面积公式可求出结果.
(I)设椭圆的方程为![]() ,则
,则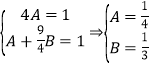
所以椭圆的标准方程 ![]() ,所以
,所以![]() ,离心率
,离心率![]()
(Ⅱ)证明:不妨设点![]() 、
、![]() 位于
位于![]() 轴的上方,则直线
轴的上方,则直线![]() 的斜率存在,
的斜率存在,
设![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() .
.
联立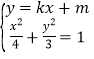 ,得
,得![]()
![]() ,
,
则![]() ,
, ![]() . ①
. ①
由![]() ,得
,得![]()
由①、②,得![]() . ③
. ③
设原点到直线![]() 的距离为
的距离为![]() ,
,![]()
![]() ,
,
![]()
![]()
![]() ④
④
由③、④,得![]() ,故四边形
,故四边形![]() 的面积为定值,且定值为
的面积为定值,且定值为![]() .
.

【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: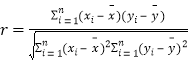 ,回归直线方程是
,回归直线方程是![]() ,
,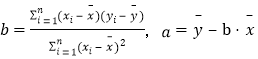 ,
,
【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有6张奖券,其中一张印有900元字样,两张印有600元字样,三张印有300元字样,抽到奖券可获得相应奖金.6位客户每人随机抽取一张奖券(不放回),设6位客户中购买产品的客户人均所得奖金为![]() 元,求
元,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |