题目内容
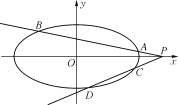
【题目】如图，在平面直角坐标系xOy中，已知焦点在x轴上，离心率为
的椭圆E的左顶点为A，点A到右准线的距离为6．
（1）求椭圆E的标准方程；
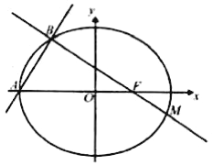
（2）过点A且斜率为
的直线与椭圆E交于点B，过点B与右焦点F的直线交椭圆E于M点，求M点的坐标．
【答案】（1）
（2）
【解析】
（1）设椭圆方程为
，由椭圆的离心率，求得
，再根据点
到右准线的距离为6，求得
，进而得到椭圆的方程；
（2）直线AB的方程为
，联立方程组，求得
或
，得到点B的坐标，得出直线BF方程，联立方程组，即可求解点M坐标。
（1）设椭圆方程为
，半焦距为c，
因为椭圆的离心率为
，所以
，即a=2c,
又因为A到右准线的距离为6，所以
，
解得a=2，c=1,所以
，所以椭圆E的标准方程为.
（2）直线AB的方程为，
由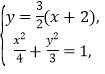
得
，解得或，
则B点的坐标为
由题意，右焦点F（1,0），所以直线BF方程为
，
由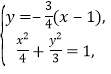
得
，解得或
，
所以，点M坐标为
.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
