题目内容
 (2013•江西)如图,椭圆C:
(2013•江西)如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.
分析:(1)由题意将点P (1,
)代入椭圆的方程,得到
+
=1(a>b>0),再由离心率为e=
,将a,b用c表示出来代入方程,解得c,从而解得a,b,即可得到椭圆的标准方程;
(2)方法一:可先设出直线AB的方程为y=k(x-1),代入椭圆的方程并整理成关于x的一元二次方程,设A(x1,y1),B(x2,y2),利用根与系数的关系求得x1+x2=
,x1x2=
,再求点M的坐标,分别表示出k1,k2,k3.比较k1+k2=λk3即可求得参数的值;
方法二:设B(x0,y0)(x0≠1),以之表示出直线FB的方程为y=
(x-1),由此方程求得M的坐标,再与椭圆方程联立,求得A的坐标,由此表示出k1,k2,k3.比较k1+k2=λk3即可求得参数的值
| 3 |
| 2 |
| 1 |
| a2 |
| 3 |
| 4b2 |
| 1 |
| 2 |
(2)方法一:可先设出直线AB的方程为y=k(x-1),代入椭圆的方程并整理成关于x的一元二次方程,设A(x1,y1),B(x2,y2),利用根与系数的关系求得x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
方法二:设B(x0,y0)(x0≠1),以之表示出直线FB的方程为y=
| y0 |
| x0-1 |
解答: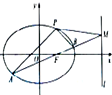 解:(1)椭圆C:
解:(1)椭圆C:
+
=1(a>b>0)经过点P (1,
),可得
+
=1(a>b>0) ①
由离心率e=
得
=
,即a=2c,则b2=3c2②,代入①解得c=1,a=2,b=
故椭圆的方程为
+
=1
(2)方法一:由题意可设AB的斜率为k,则直线AB的方程为y=k(x-1)③
代入椭圆方程
+
=1并整理得(4k2+3)x2-8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),
x1+x2=
,x1x2=
④
在方程③中,令x=4得,M的坐标为(4,3k),
从而k1=
,k2=
,k3=
=k-
注意到A,F,B共线,则有k=kAF=kBF,即有
=
=k
所以k1+k2=
+
=
+
-
(
+
)
=2k-
×
⑤
④代入⑤得k1+k2=2k-
×
=2k-1
又k3=k-
,所以k1+k2=2k3
故存在常数λ=2符合题意
方法二:设B(x0,y0)(x0≠1),则直线FB的方程为y=
(x-1)
令x=4,求得M(4,
)
从而直线PM的斜率为k3=
,
联立
,得A(
,
),
则直线PA的斜率k1=
,直线PB的斜率为k2=
所以k1+k2=
+
=2×
=2k3,
故存在常数λ=2符合题意
 解:(1)椭圆C:
解:(1)椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| a2 |
| 9 |
| 4b2 |
由离心率e=
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| 3 |
故椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)方法一:由题意可设AB的斜率为k,则直线AB的方程为y=k(x-1)③
代入椭圆方程
| x2 |
| 4 |
| y2 |
| 3 |
设A(x1,y1),B(x2,y2),
x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
在方程③中,令x=4得,M的坐标为(4,3k),
从而k1=
y1-
| ||
| x1-1 |
y2-
| ||
| x2-1 |
3k-
| ||
| 4-1 |
| 1 |
| 2 |
注意到A,F,B共线,则有k=kAF=kBF,即有
| y1 |
| x1-1 |
| y2 |
| x2-1 |
所以k1+k2=
y1-
| ||
| x1-1 |
y2-
| ||
| x2-1 |
| y1 |
| x1-1 |
| y2 |
| x2-1 |
| 3 |
| 2 |
| 1 |
| x1-1 |
| 1 |
| x2-1 |
=2k-
| 3 |
| 2 |
| x1+x2-2 |
| x1x2-(x1+x2)+1 |
④代入⑤得k1+k2=2k-
| 3 |
| 2 |
| ||||
|
又k3=k-
| 1 |
| 2 |
故存在常数λ=2符合题意
方法二:设B(x0,y0)(x0≠1),则直线FB的方程为y=
| y0 |
| x0-1 |
令x=4,求得M(4,
| 3y0 |
| x0-1 |
从而直线PM的斜率为k3=
| 2y0-x0+1 |
| 2(x0-1) |
联立
|
| 5x0-8 |
| 2x0-5 |
| 3x0 |
| 2x0-5 |
则直线PA的斜率k1=
| 2y0-2x0+5 |
| 2(x0-1) |
| 2y0-3 |
| 2(x0-1) |
所以k1+k2=
| 2y0-2x0+5 |
| 2(x0-1) |
| 2y0-3 |
| 2(x0-1) |
| 2y0-x0+1 |
| 2(x0-1) |
故存在常数λ=2符合题意
点评:本题考查直线与圆锥曲线的综合问题,考查了分析转化的能力与探究的能力,考查了方程的思想,数形结合的思想,本题综合性较强,运算量大,极易出错,解答时要严谨运算,严密推理,方能碸解答出.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
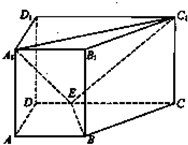 (2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
(2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=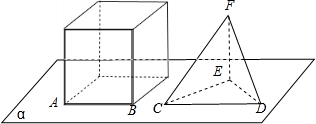 (2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为
(2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为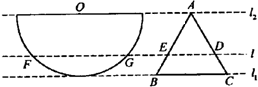 (2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
(2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
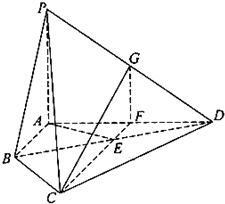 (2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
(2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=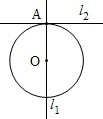 (2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
(2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )