题目内容
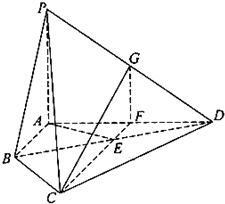 (2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
(2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=| 3 | 2 |
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
分析:(1)利用直角三角形的判定得到∠BAD=
,且∠ABE=∠AEB=
.由△DAB≌△DCB得到△EAB≌△ECB,从而得到∠FED=∠FEA=
,所以EF⊥AD且AF=FD,结合题意得到FG是△PAD是的中位线,可得FG∥PA,根据PA⊥平面ABCD得FG⊥平面ABCD,得到FG⊥AD,最后根据线面垂直的判定定理证出AD⊥平面CFG;
(2)以点A为原点,AB、AD、PA分别为x轴、y轴、z轴建立如图直角坐标系,得到A、B、C、D、P的坐标,从而得到
、
、
的坐标,利用垂直向量数量积为零的方法建立方程组,解出
=(1,-
,
)和
=(1,
,2)分别为平面BCP、平面DCP的法向量,利用空间向量的夹角公式算出
、
夹角的余弦,即可得到平面BCP与平面DCP的夹角的余弦值.
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
(2)以点A为原点,AB、AD、PA分别为x轴、y轴、z轴建立如图直角坐标系,得到A、B、C、D、P的坐标,从而得到
| BC |
| CP |
| CD |
| m |
| ||
| 3 |
| 2 |
| 3 |
| n |
| 3 |
| m |
| n |
解答: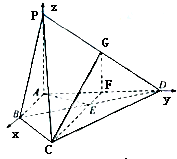 解:(1)∵在△DAB中,E为BD的中点,EA=EB=AB=1,
解:(1)∵在△DAB中,E为BD的中点,EA=EB=AB=1,
∴AE=
BD,可得∠BAD=
,且∠ABE=∠AEB=
∵△DAB≌△DCB,∴△EAB≌△ECB,从而得到∠FED=∠BEC=∠AEB=
∴∠FED=∠FEA=
,可得EF⊥AD,AF=FD
又∵△PAD中,PG=GD,∴FG是△PAD是的中位线,可得FG∥PA
∵PA⊥平面ABCD,∴FG⊥平面ABCD,
∵AD?平面ABCD,∴FG⊥AD
又∵EF、FG是平面CFG内的相交直线,∴AD⊥平面CFG;
(2)以点A为原点,AB、AD、PA分别为x轴、y轴、z轴建立如图直角坐标系,可得
A(0,0,0),B(1,0,0),C(
,
,0),D(0,
,0),P(0,0,
)
∴
=(
,
,0),
=(-
,-
,
),
=(-
,
,0)
设平面BCP的法向量
=(1,y1,z1),则
解得y1=-
,z1=
,可得
=(1,-
,
),
设平面DCP的法向量
=(1,y2,z2),则
解得y2=
,z2=2,可得
=(1,
,2),
∴cos<
,
>=
=
=
因此平面BCP与平面DCP的夹角的余弦值等于|cos<
,
>|=
.
 解:(1)∵在△DAB中,E为BD的中点,EA=EB=AB=1,
解:(1)∵在△DAB中,E为BD的中点,EA=EB=AB=1,∴AE=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
∵△DAB≌△DCB,∴△EAB≌△ECB,从而得到∠FED=∠BEC=∠AEB=
| π |
| 3 |
∴∠FED=∠FEA=
| π |
| 3 |
又∵△PAD中,PG=GD,∴FG是△PAD是的中位线,可得FG∥PA
∵PA⊥平面ABCD,∴FG⊥平面ABCD,
∵AD?平面ABCD,∴FG⊥AD
又∵EF、FG是平面CFG内的相交直线,∴AD⊥平面CFG;
(2)以点A为原点,AB、AD、PA分别为x轴、y轴、z轴建立如图直角坐标系,可得
A(0,0,0),B(1,0,0),C(
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∴
| BC |
| 1 |
| 2 |
| ||
| 2 |
| CP |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| CD |
| 3 |
| 2 |
| ||
| 2 |
设平面BCP的法向量
| m |
|
解得y1=-
| ||
| 3 |
| 2 |
| 3 |
| m |
| ||
| 3 |
| 2 |
| 3 |
设平面DCP的法向量
| n |
|
解得y2=
| 3 |
| n |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
1×1+(-
| ||||||||
|
| ||
| 4 |
因此平面BCP与平面DCP的夹角的余弦值等于|cos<
| m |
| n |
| ||
| 4 |
点评:本题在三棱锥中求证线面垂直,并求平面与平面所成角的余弦值.着重考查了空间线面垂直的判定与性质,考查了利用空间向量研究平面与平面所成角等知识,属于中档题.

练习册系列答案
相关题目
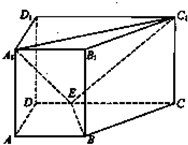 (2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
(2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=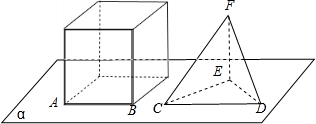 (2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为
(2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为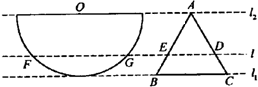 (2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
(2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
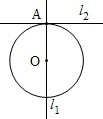 (2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
(2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )