题目内容
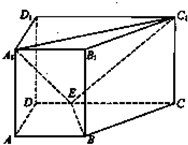 (2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
(2013•江西)如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=| 2 |
(1)证明:BE⊥平面BB1C1C;
(2)求点B1到平面EA1C1 的距离.
分析:(1)过点B作BF⊥CD于F点,算出BF、EF、FC的长,从而在△BCE中算出BE、BC、CE的长,由勾股定理的逆定理得BE⊥BC,结合BE⊥BB1利用线面垂直的判定定理,可证出BE⊥平面BB1C1C;
(2)根据AA1⊥平面A1B1C1,算出三棱锥E-A1B1C1的体积V=
.根据线面垂直的性质和勾股定理,算出A1C1=EC1=3
、A1E=2
,从而得到等腰△A1EC1的面积S△ A1E C1=3
,设B1到平面EA1C1 的距离为d,可得三棱锥B1-A1C1E的体积V=
×S△ A1E C1×d=
d,从而得到
=
d,由此即可解出点B1到平面EA1C1 的距离.
(2)根据AA1⊥平面A1B1C1,算出三棱锥E-A1B1C1的体积V=
| 2 |
| 2 |
| 3 |
| 5 |
| 1 |
| 3 |
| 5 |
| 2 |
| 5 |
解答: 解:(1)过点B作BF⊥CD于F点,则
解:(1)过点B作BF⊥CD于F点,则
BF=AD=
,EF=AB=DE=1,FC=2
在Rt△BEF中,BE=
=
;在Rt△BCF中,BC=
=
因此,△BCE中可得BE2+BC2=9=CE2
∴∠CBE=90°,可得BE⊥BC,
∵BB1⊥平面ABCD,BE?平面ABCD,∴BE⊥BB1,
∵BC、BB1是平面BB1C1C内的相交直线,∴BE⊥平面BB1C1C;
(2)∵AA1⊥平面A1B1C1,得AA1是三棱锥E-A1B1C1的高线
∴三棱锥E-A1B1C1的体积V=
×AA1×S△ A1B1C1=
在Rt△A1D1C1中,A1C1=
=3
同理可得EC1=
=3
,A1E=
=2
∴等腰△A1EC1的底边EC1上的中线等于
=
,
可得S△ A1E C1=
×2
×
=3
设点B1到平面EA1C1 的距离为d,则三棱锥B1-A1C1E的体积为
V=
×S△ A1E C1×d=
d,可得
=
d,解之得d=
即点B1到平面EA1C1 的距离为
.
 解:(1)过点B作BF⊥CD于F点,则
解:(1)过点B作BF⊥CD于F点,则BF=AD=
| 2 |
在Rt△BEF中,BE=
| BF2+EF2 |
| 3 |
| BF2+CF2 |
| 6 |
因此,△BCE中可得BE2+BC2=9=CE2
∴∠CBE=90°,可得BE⊥BC,
∵BB1⊥平面ABCD,BE?平面ABCD,∴BE⊥BB1,
∵BC、BB1是平面BB1C1C内的相交直线,∴BE⊥平面BB1C1C;
(2)∵AA1⊥平面A1B1C1,得AA1是三棱锥E-A1B1C1的高线
∴三棱锥E-A1B1C1的体积V=
| 1 |
| 3 |
| 2 |
在Rt△A1D1C1中,A1C1=
| A1D12+D 1C12 |
| 2 |
同理可得EC1=
| E C 2+C C12 |
| 2 |
| A1A2+AD2+DE2 |
| 3 |
∴等腰△A1EC1的底边EC1上的中线等于
(3
|
| 15 |
可得S△ A1E C1=
| 1 |
| 2 |
| 3 |
| 15 |
| 5 |
设点B1到平面EA1C1 的距离为d,则三棱锥B1-A1C1E的体积为
V=
| 1 |
| 3 |
| 5 |
| 2 |
| 5 |
| ||
| 5 |
即点B1到平面EA1C1 的距离为
| ||
| 5 |
点评:本题在直四棱柱中求证线面垂直,并求点到平面的距离.着重考查了线面垂直的判定与性质、勾股定理与其逆定理和利用等积转换的方法求点到平面的距离等知识,属于中档题.

练习册系列答案
相关题目
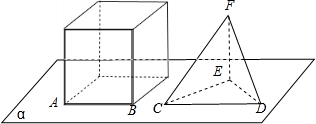 (2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为
(2013•江西)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为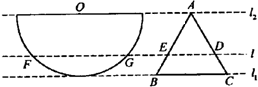 (2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
(2013•江西)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
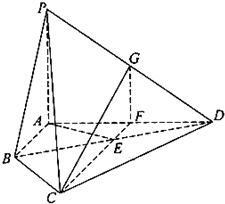 (2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
(2013•江西)如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=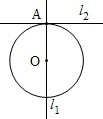 (2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
(2013•江西)如图.已知l1⊥l2,圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )