题目内容
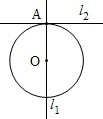（2013•江西）如图．已知l1⊥l2，圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A，圆O沿l1以1m/s的速度匀速向上移动，圆被直线l2所截上方圆弧长记为x，令y=cosx，则y与时间t（0≤t≤1，单位：s）的函数y=f（t）的图象大致为（ ）分析：通过t的增加，排除选项A、D，利用x的增加的变化率，说明余弦函数的变化率，得到选项即可．
解答：解：因为当t=0时，x=0，对应y取得1，所以选项A，D不合题意，
当t由0增加时，x的变化率由大变小，又y=cosx是减函数，所以函数y=f（t）的图象变化先快后慢，
所以选项B满足题意，C正好相反．
故选B．
当t由0增加时，x的变化率由大变小，又y=cosx是减函数，所以函数y=f（t）的图象变化先快后慢，
所以选项B满足题意，C正好相反．
故选B．
点评：本题考查函数图象的变换快慢，考查学生理解题意以及视图能力．
练习册系列答案
相关题目
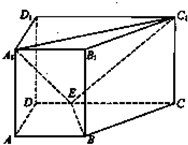（2013•江西）如图，直四棱柱ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=
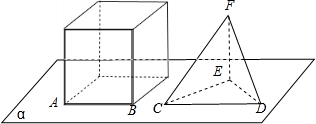（2013•江西）如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数为
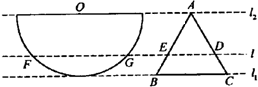（2013•江西）如图，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点．设弧
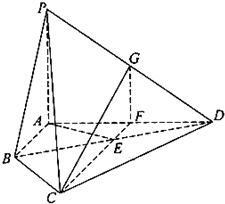（2013•江西）如图，四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB≌△DCB，EA=EB=AB=1，PA=