题目内容
【题目】若函数 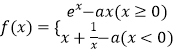 没有零点,则实数a的取值范围是 .
没有零点,则实数a的取值范围是 .
【答案】(﹣2,e)
【解析】解:当x<0时, ![]() ,
,
当x∈(﹣∞,﹣1)时,f'(x)>0,f(x)单调递增,
当x∈(﹣1,0)时,f'(x)<0,f(x)单调递减,
所以当x=﹣1时,f(x)取得极大值f(﹣1)=﹣2﹣a,根据题意,﹣2﹣a<0,a>﹣2;
当x≥0时,f'(x)=ex﹣a,当a∈(﹣2,1]时,f'(x)≥0,f(x)单调递增,
所以fmin(x)=f(0)=1>0,满足题意;
当a>1时,令f'(x)=0,得x=lna,
当x∈[0,lna)时,f'(x)<0,f(x)单调递减,
当x∈(lna,+∞)时,f'(x)>0,f(x)单调递增,
所以当x=lna时,f(x)取得极大值f(lna)=a﹣alna,根据题意,a﹣alna>0,
所以1﹣lna>0,lna<1,a<e,
∴a∈(1,e),
综上所述,实数a的取值范围是(﹣2,e).
故答案为:(﹣2,e).
在分段函数上根据不同的解析式进行讨论,求导根据单调性,得出极值,可得a的取值范围.

练习册系列答案
相关题目