Question

【题目】在平面直角坐标系中．以原点为极点，x轴的正半轴为极轴建立极坐标系已知曲线C：pcos2θ=2asinθ（a＞0）过点P（﹣4，﹣2）的直线l的参数方程为 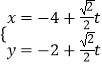（t为参数）直线l与曲线C分别交于点M，N．
（1）写出C的直角坐标方程和l的普通方程；
（2）若丨PM丨，丨MN丨，丨PN丨成等比数列，求a的值．

Answer 1

【答案】
（1）解：曲线C的直角坐标方程为x=2ay（a＞0），

直线l的普通方程为x﹣y+2=0．

（2）将直线l的参数方程与C的直角坐标方程联立，得t2﹣2 （4+a）t+8（4+a）=0．

由△=8a（4+a）＞0，

可设点M，N对应的参数分别为t1，t2，且t1，t2是方程（*）的根，

则丨PM丨=丨t1丨，丨PN丨=丨t2丨，丨MN丨=丨t1﹣t2丨．

由题设得（t1﹣t2）2=丨t1t2丨，即（t1﹣t2）2﹣4t1t2=丨t1t2丨．

由（*）得t1+t2=2 （4+a），t1t2=8（4+a）＞0，

则有（4+a）2﹣5（4+a）=0，解得a=1或a=﹣4．

因为a＞0，则a=1．

【解析】（1）对于曲线C的极坐标方程，两边同时乘以ρ，再化为平面直角坐标方程，通过加减消参可得出直线的直角坐标方程；（2）将直线l的参数方程代入C的直角坐标方程，根据t的几何意义，表示出PM，PN、MN，结合韦达定理可解出a的值.