题目内容
16．若函数f（x-1）=$\sqrt{x+2}$+$\frac{1}{x+1}$，求f（x）．分析 先求出x的范围，利用换元法求函数的解析式即可．
解答 解：由x+2≥0且x+1≠0，
解得：x≥-2且x≠-1，
令x-1=t，则x=t+1，
∴t≥-3且t≠-2，
∴f（t）=$\sqrt{t+1+2}$+$\frac{1}{t+1+1}$
=$\sqrt{t+3}$+$\frac{1}{t+2}$，
∴f（x）=$\sqrt{x+3}$+$\frac{1}{x+2}$，（x≥-3且x≠-2）．
点评 本题考查了求函数的解析式问题，换元法是常用方法之一，本题是一道基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
11．
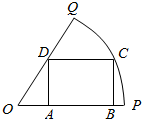如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）
如图所示，扇形OPQ的半径为2，圆心角为$\frac{π}{3}$，C是扇形弧上的动点，四边形ABCD是扇形的内接矩形，则SABCD的最大值是（ ）| A． | $\frac{2\sqrt{3}}{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | $\frac{2}{3}$ |