题目内容
【题目】已知海岛
在海岛
北偏东
，，相距
海里，物体甲从海岛以
海里/小时的速度沿直线向海岛移动，同时物体乙从海岛沿着海岛北偏西
方向以
海里/小时的速度移动．
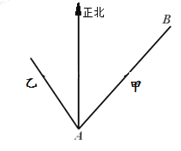
（1）问经过多长时间，物体甲在物体乙的正东方向；
（2）求甲从海岛到达海岛的过程中，甲、乙两物体的最短距离．
【答案】（1）
小时；（2）
海里．
【解析】
试题（1）设经过
小时，物体甲在物体乙的正东方向，因为
小时，所以
．则物体甲与海岛
的距离为
海里，物体乙与海岛距离为
海里．在
中由正弦定理可求得的值．（2）在中用余弦定理求
，再根据二次函数求的最小值．
试题解析：解：
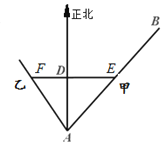
（1）设经过
小时，物体甲在物体乙的正东方向．如图所示，物体甲与海岛的距离为海里，物体乙与海岛距离为海里，
，
中，由正弦定理得：
，即
，
则
．
（2）由（1）题设，
，，
由余弦定理得：
∵，
∴当
时，
海里．
【题目】某销售公司拟招聘一名产品推销员，有如下两种工资方案：
方案一：每月底薪2000元，每销售一件产品提成15元；
方案二：每月底薪3500元，月销售量不超过300件，没有提成，超过300件的部分每件提成30元．
（1）分别写出两种方案中推销员的月工资
（单位：元）与月销售产品件数
的函数关系式；
（2）从该销售公司随机选取一名推销员，对他（或她）过去两年的销售情况进行统计，得到如下统计表：
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率，分别求两种方案推销员的月工资超过11090元的概率．
【题目】为了解甲、乙两奶粉厂的产品质量，采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件，测量产品中微量元素
的含量（单位：毫克）．下表是乙厂的5件产品的测量数据：
编号 | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
（1）已知甲厂生产的产品共有96件，求乙厂生产的产品数量；
（2）当产品中的微量元素满足
且
时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量；
（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数
的分布列及其均值（即数学期望）．
