题目内容
在平面直角坐标系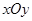 中,直线l与抛物线
中,直线l与抛物线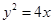 相交于不同的两点A,B.
相交于不同的两点A,B.
(I)如果直线l过抛物线的焦点,求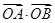 的值;
的值;
(II)如果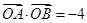 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.
(I)-3.(II)直线l过定点(2,0).
解析试题分析:(I)注意到抛物线的焦点为(1,0),因此可设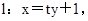 并代入抛物线y2=4x中消去
并代入抛物线y2=4x中消去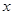 ,
,
设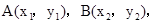 应用韦达定理得到
应用韦达定理得到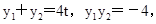 从而易于将
从而易于将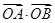 用坐标表示.
用坐标表示.
(II)设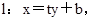 代入方程
代入方程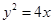 消去
消去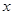 得,
得,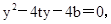 设
设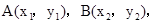 得到
得到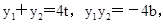 .
.
将 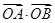 用坐标表示,得到
用坐标表示,得到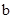 的方程,通过确定
的方程,通过确定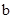 ,达到证明直线过定点的目的.
,达到证明直线过定点的目的.
试题解析:(I)由题意知,抛物线的焦点为(1,0),
设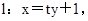 代入抛物线
代入抛物线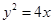 中消去x得,
中消去x得,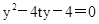 ,设
,设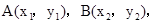 则
则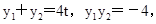
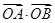 =
=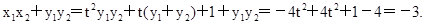 6分
6分
(II)设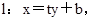 代入方程
代入方程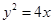 消去
消去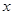 得,
得,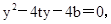 设
设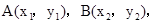 得到
得到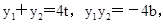
∵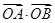 =
=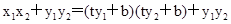 =
=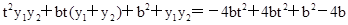 =b2-4b.
=b2-4b.
令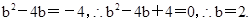 ∴直线l过定点(2,0). 12分
∴直线l过定点(2,0). 12分
考点:抛物线的几何性质,直线与抛物线的位置关系.

练习册系列答案
相关题目
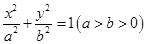 过点(0,4),离心率为
过点(0,4),离心率为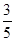
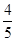 的直线被C所截线段的长度.
的直线被C所截线段的长度.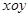 上取两个定点
上取两个定点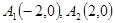 ,再取两个动点
,再取两个动点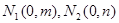 且
且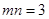 .
.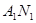 与
与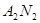 交点的轨迹
交点的轨迹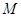 的方程;
的方程;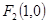 ,设直线:
,设直线: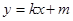 与(I)中的轨迹
与(I)中的轨迹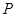 、
、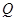 两点,直线
两点,直线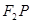 、
、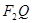 的倾斜角分别为
的倾斜角分别为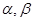 且
且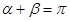 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.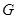 :
: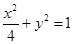 ,过点
,过点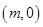 作圆
作圆 的切线
的切线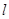 交椭圆
交椭圆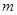 的取值范围;
的取值范围;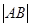 表示为
表示为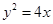 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点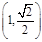 .
.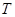
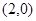 ,过点F2作直线
,过点F2作直线 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且 ,若
,若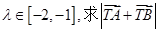 的取值范围.
的取值范围.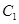 的参数方程为
的参数方程为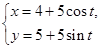 (
(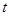 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线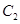 的极坐标方程为
的极坐标方程为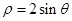 .
.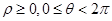 ).
).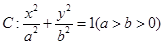 的离心率为
的离心率为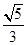 ,定点
,定点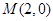 ,椭圆短轴的端点是
,椭圆短轴的端点是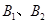 ,且
,且 .
.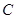 的方程;
的方程; 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆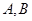 两点.试问
两点.试问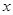 轴上是否存在异于
轴上是否存在异于 ,使
,使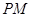 平分
平分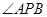 ?若存在,求出点
?若存在,求出点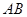 长为2m,跳水板距水面
长为2m,跳水板距水面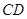 的高
的高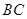 为3m,
为3m, =5m,
=5m,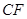 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(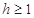 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以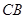 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.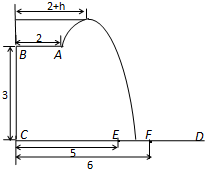
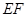 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时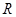 :
: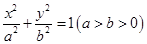 的长轴长为4,且过点
的长轴长为4,且过点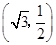 .
. 、
、 、
、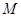 是椭圆上的三点,若
是椭圆上的三点,若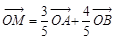 ,点
,点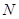 为线段
为线段 的中点,
的中点, 、
、 两点的坐标分别为
两点的坐标分别为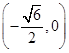 、
、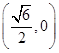 ,求证:
,求证: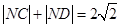 .
.