题目内容
在直角坐标系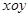 上取两个定点
上取两个定点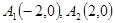 ,再取两个动点
,再取两个动点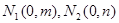 且
且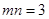 .
.
(I)求直线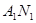 与
与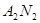 交点的轨迹
交点的轨迹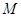 的方程;
的方程;
(II)已知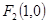 ,设直线:
,设直线: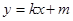 与(I)中的轨迹
与(I)中的轨迹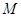 交于
交于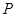 、
、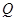 两点,直线
两点,直线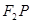 、
、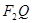 的倾斜角分别为
的倾斜角分别为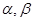 且
且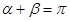 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.
(I) ;(II)定点为
;(II)定点为 .
.
解析试题分析:(I)已知条件是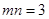 ,因此我们可以设直线
,因此我们可以设直线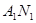 与
与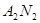 交点
交点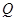 的坐标为
的坐标为 ,把
,把 与
与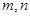 建立起联系,利用已知
建立起联系,利用已知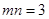 得到交点
得到交点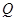 的轨迹方程,而这个联系就是直线
的轨迹方程,而这个联系就是直线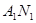 与
与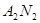 的方程;(II)要证明直线过定点,应该求出
的方程;(II)要证明直线过定点,应该求出 的关系,而已知的是直线
的关系,而已知的是直线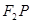 、
、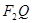 的倾斜角
的倾斜角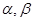 且
且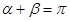 ,说明它们的斜率之和为0,设直线
,说明它们的斜率之和为0,设直线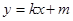 与轨迹
与轨迹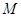 的交点为
的交点为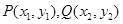 ,则
,则 ,
, ,那么
,那么 ,变形得
,变形得 ,这里
,这里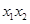 ,
,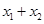 可由直线
可由直线 与轨迹
与轨迹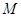 的方程联立,消去
的方程联立,消去 得关于
得关于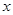 的二次方程,由韦达定理得到
的二次方程,由韦达定理得到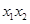 ,
,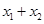 ,代入上式可得到结论.
,代入上式可得到结论.
试题解析:(I)依题意知直线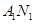 的方程为:
的方程为: ①,
①,
直线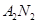 的方程为:
的方程为: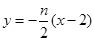 ②,
②,
设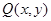 是直线
是直线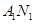 与
与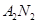 的交点,①×②得
的交点,①×②得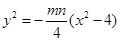 ,
,
由 整理得
整理得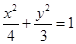 ,
,
∵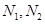 不与原点为重合,∴点
不与原点为重合,∴点 不在轨迹M上,
不在轨迹M上,
∴轨迹M的方程为 .
.
(II)由题意知,直线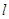 的斜率存在且不为零,
的斜率存在且不为零,
联立方程 ,得
,得 ,设
,设 、
、 则
则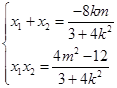 ,且
,且 ,
, ,
,
由已知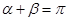 ,得
,得 ,∴
,∴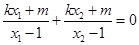 ,
,
化简得 ,
,
代入得 ,整理得
,整理得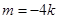 .
.
∴直线 的方程为
的方程为 ,因此直线
,因此直线 过定点,该定点的坐标为
过定点,该定点的坐标为 .
.
考点:(I)动点转移法求轨迹方程;(II)直线和椭圆相交问题.

练习册系列答案
相关题目
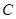 :
: ,
,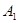 、
、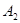 、
、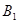 、
、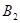 为椭圆
为椭圆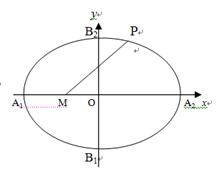
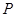 到焦点距离的最大值为
到焦点距离的最大值为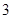 ,最小值为
,最小值为 ,求椭圆方程;
,求椭圆方程;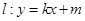 相交于
相交于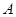 ,
,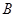 两点(
两点(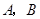 不是椭圆的左右顶点),并满足
不是椭圆的左右顶点),并满足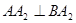 试研究:直线
试研究:直线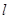 是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由
是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由 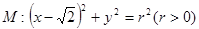 ,若椭圆
,若椭圆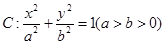 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为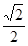 .
. 的方程;
的方程;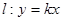 ,使得直线
,使得直线 与椭圆
与椭圆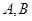 两点,与圆
两点,与圆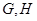 两点,点
两点,点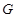 在线段
在线段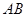 上,且
上,且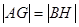 ,求圆
,求圆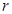 的取值范围.
的取值范围. 的顶点为原点,其焦点
的顶点为原点,其焦点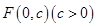 到直线
到直线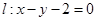 的距离为
的距离为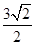 .设
.设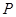 为直线
为直线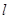 上的点,过点
上的点,过点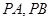 ,其中
,其中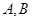 为切点.
为切点.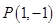 为直线
为直线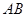 的方程;
的方程; 在直线
在直线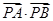 的最小值.
的最小值.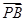 |,
|, |
|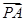 |,8成等差数列.
|,8成等差数列.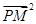 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?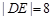 ,动点C的运动轨迹为曲线G,且当动点C运动时,
,动点C的运动轨迹为曲线G,且当动点C运动时,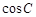 有最小值
有最小值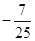 .
.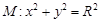 (其中
(其中 )于A、B两点,求|AB|的取值范围.
)于A、B两点,求|AB|的取值范围. 轴上方有一段曲线弧
轴上方有一段曲线弧 ,其端点
,其端点 、
、 在
在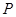 及点
及点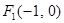 ,
,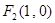 ,满足:
,满足: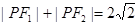 .直线
.直线 ,
,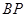 分别交直线
分别交直线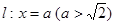 于
于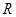 ,
,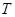 两点.
两点.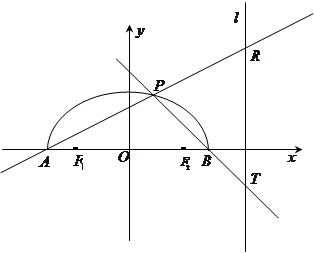
 的最小值(用
的最小值(用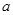 表示);
表示);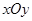 中,直线l与抛物线
中,直线l与抛物线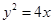 相交于不同的两点A,B.
相交于不同的两点A,B.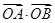 的值;
的值;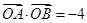 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.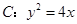 焦点为
焦点为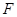 ,直线
,直线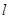 经过点
经过点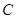 相交于
相交于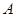 ,
,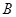 两点
两点 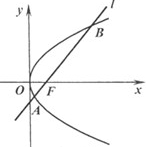
 的中点在直线
的中点在直线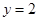 上,求直线
上,求直线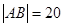 ,求直线
,求直线