题目内容
知椭圆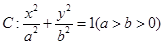 的离心率为
的离心率为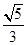 ,定点
,定点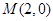 ,椭圆短轴的端点是
,椭圆短轴的端点是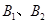 ,且
,且 .
.
(1)求椭圆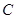 的方程;
的方程;
(2)设过点 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆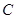 于
于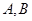 两点.试问
两点.试问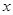 轴上是否存在异于
轴上是否存在异于 的定点
的定点 ,使
,使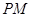 平分
平分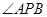 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)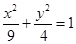 ;(2)存在,
;(2)存在,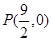 .
.
解析试题分析:(1)由离心率为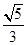 可得到一个关于
可得到一个关于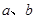 的方程,再根据MB1⊥MB2即可得
的方程,再根据MB1⊥MB2即可得 ;(2)本题采用“设而不求”的方法,将A,B两点坐标设出,但不求出.注意到
;(2)本题采用“设而不求”的方法,将A,B两点坐标设出,但不求出.注意到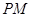 平分
平分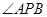 ,则直线
,则直线 的倾斜角互补这个性质,从而由斜率着手,以韦达定理为辅助工具,得出点P的坐标.
的倾斜角互补这个性质,从而由斜率着手,以韦达定理为辅助工具,得出点P的坐标.
试题解析:(1)由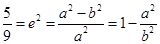 得
得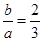
又 ,知
,知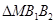 是等腰直角三角形,从而
是等腰直角三角形,从而 .
.
所以椭圆C的方程是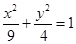 . 5分
. 5分
(2)设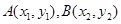 ,直线AB的方程为
,直线AB的方程为
由 得
得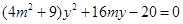 ,
,
所以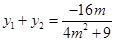 ①,
①,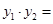
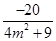 ② 8分
② 8分
若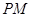 平分
平分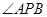 ,则直线
,则直线 的倾斜角互补,
的倾斜角互补,
所以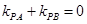
设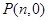 ,则有
,则有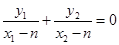 , 10分
, 10分
将 代入上式,整理得
代入上式,整理得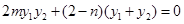 ,
,
将①②代入得 ,由于上式对任意实数都成立,所以
,由于上式对任意实数都成立,所以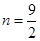 .
.
综上,存在定点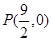 ,使平分PM平分∠APB. 13分
,使平分PM平分∠APB. 13分
考点:1.椭圆的简单几何性质;2.直线与圆锥曲线的位置关系;3.斜率公式.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
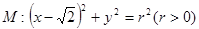 ,若椭圆
,若椭圆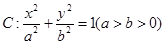 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为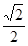 .
. 的方程;
的方程;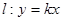 ,使得直线
,使得直线 与椭圆
与椭圆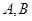 两点,与圆
两点,与圆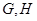 两点,点
两点,点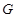 在线段
在线段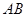 上,且
上,且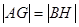 ,求圆
,求圆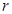 的取值范围.
的取值范围. 轴上方有一段曲线弧
轴上方有一段曲线弧 ,其端点
,其端点 、
、 在
在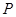 及点
及点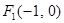 ,
,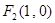 ,满足:
,满足: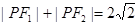 .直线
.直线 ,
,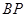 分别交直线
分别交直线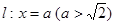 于
于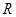 ,
,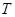 两点.
两点.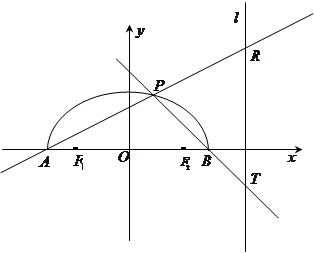
 的最小值(用
的最小值(用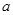 表示);
表示);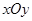 中,直线l与抛物线
中,直线l与抛物线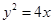 相交于不同的两点A,B.
相交于不同的两点A,B.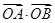 的值;
的值;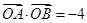 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.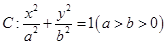 过点
过点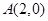 ,离心率为
,离心率为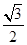 .
.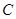 的方程;
的方程;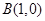 且斜率为
且斜率为 (
(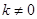 )的直线
)的直线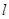 与椭圆
与椭圆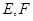 两点,直线
两点,直线 、
、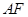 分别交直线
分别交直线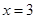 于
于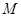 、
、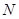 两点,线段
两点,线段 的中点为
的中点为 .记直线
.记直线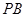 的斜率为
的斜率为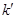 ,求证:
,求证: 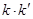 为定值.
为定值. ,0),B(
,0),B( 的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.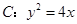 焦点为
焦点为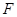 ,直线
,直线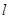 经过点
经过点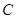 相交于
相交于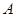 ,
,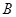 两点
两点 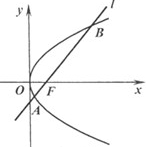
 的中点在直线
的中点在直线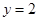 上,求直线
上,求直线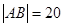 ,求直线
,求直线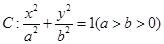 的左、右焦点分别为
的左、右焦点分别为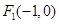 、
、 ,P为椭圆
,P为椭圆 上任意一点,且
上任意一点,且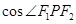 的最小值为
的最小值为 .
.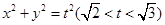 与椭圆
与椭圆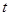 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.