题目内容
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板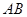 长为2m,跳水板距水面
长为2m,跳水板距水面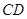 的高
的高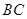 为3m,
为3m, =5m,
=5m,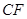 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(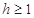 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以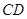 为横轴,
为横轴,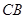 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.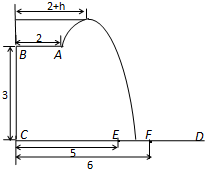
(1)当 =1时,求跳水曲线所在的抛物线方程;
=1时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域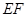 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时 的取值范围.
的取值范围.
(1)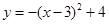 ;(2)
;(2)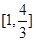 .
.
解析试题分析:(1)由题意可以将抛物线的方程设为顶点式.由顶点(3,4),然后代入点 可将抛物线方程求出;(2)将抛物线的方程设为顶点式,由点
可将抛物线方程求出;(2)将抛物线的方程设为顶点式,由点 得
得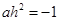 .将
.将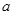 用
用 表示.跳水运动员在区域
表示.跳水运动员在区域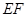 内入水时才能达到压水花的训练要求,所以方程
内入水时才能达到压水花的训练要求,所以方程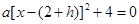 在区间[5,6]内有一解,根据抛物线开口向下,由函数的零点与方程的根的关系,令
在区间[5,6]内有一解,根据抛物线开口向下,由函数的零点与方程的根的关系,令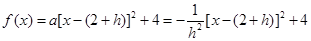 ,由
,由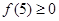 ,且
,且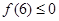 可得
可得 的取值范围.
的取值范围.
试题解析:(1)由题意知最高点为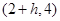 ,
,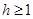 ,
,
设抛物线方程为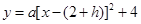 , 4分
, 4分
当 时,最高点为(3,4),方程为
时,最高点为(3,4),方程为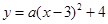 ,
,
将 代入,得
代入,得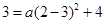 ,
,
解得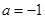 .
.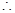 当
当 时,跳水曲线所在的抛物线方程
时,跳水曲线所在的抛物线方程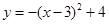 . 8分
. 8分
(2)将点 代入
代入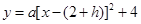
得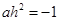 ,所以
,所以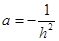 .
.
由题意,方程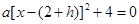 在区间[5,6]内有一解. 10分
在区间[5,6]内有一解. 10分
令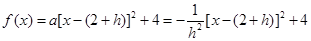 ,
,
则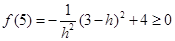 ,且
,且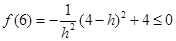 .
.
解得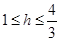 . 14分
. 14分
达到压水花的训练要求时 的取值范围
的取值范围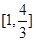 . 16分
. 16分
考点:1.抛物线的顶点式方程;2.函数的零点与方程的根.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 的顶点为原点,其焦点
的顶点为原点,其焦点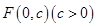 到直线
到直线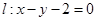 的距离为
的距离为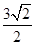 .设
.设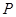 为直线
为直线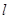 上的点,过点
上的点,过点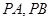 ,其中
,其中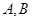 为切点.
为切点.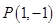 为直线
为直线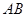 的方程;
的方程; 在直线
在直线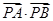 的最小值.
的最小值.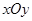 中,直线l与抛物线
中,直线l与抛物线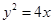 相交于不同的两点A,B.
相交于不同的两点A,B.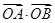 的值;
的值;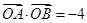 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标. ,0),B(
,0),B( 的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.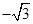 ,0),B(
,0),B(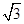 ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为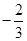 .
.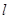 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转,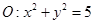 相交于P、Q两点,
相交于P、Q两点,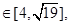 求△
求△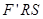 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点).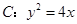 焦点为
焦点为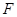 ,直线
,直线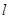 经过点
经过点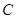 相交于
相交于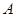 ,
,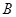 两点
两点 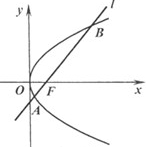
 的中点在直线
的中点在直线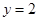 上,求直线
上,求直线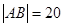 ,求直线
,求直线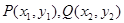 是抛物线
是抛物线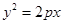
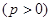 上相异两点,
上相异两点,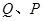 到y轴的距离的积为
到y轴的距离的积为 且
且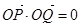 .
.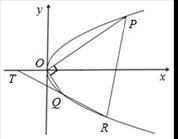
 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值. 在
在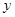 轴右边,
轴右边,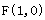 的距离减去它到
的距离减去它到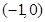 的直线
的直线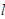 与曲线C有两个交点
与曲线C有两个交点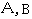 ,且
,且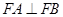 ,求直线
,求直线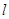 的斜率.
的斜率.