题目内容
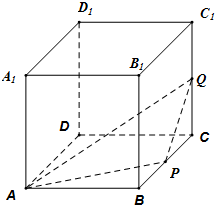 正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是
正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是①当x=0时,S为矩形,其面积最大为1;
②当x=y=
| 1 |
| 2 |
③当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| y |
④当y=1时,以B1为顶点,S为底面的棱锥的体积为定值
| 1 |
| 3 |
考点:命题的真假判断与应用,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由题意作出满足条件的图形,由线面位置关系找出截面,再判断每一个选项是否正确.
解答:
解:对于①,当x=0时,过点A,P,Q的截面S是矩形,其面积最大是1×
=
,∴①错误;
对于②,当x=y=
时,如图所示,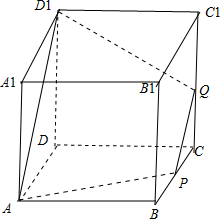
过点A,P,Q的截面S是等腰梯形,∴②正确;
对于③,当x=
,y∈(
,1)时,设S与棱C1D1的交点为R,如图,
延长DD1,使DD1∩QR=N,连接AN交A1D1于S,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N,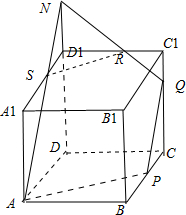
可得RD1=2-
,∴③正确;
④当y=1时,以B1为顶点,S为底面的棱锥B1-APC1M如图所示,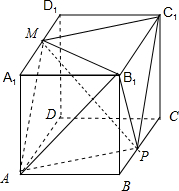
该四棱锥的体积为VB1-APC1M=2VB1-PC1M=2VP-B1C1M
=2×
×
×1×1×1=
,∴④正确.
| 2 |
| 2 |
对于②,当x=y=
| 1 |
| 2 |

过点A,P,Q的截面S是等腰梯形,∴②正确;
对于③,当x=
| 1 |
| 2 |
| 1 |
| 2 |
延长DD1,使DD1∩QR=N,连接AN交A1D1于S,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N,

可得RD1=2-
| 1 |
| y |
④当y=1时,以B1为顶点,S为底面的棱锥B1-APC1M如图所示,

该四棱锥的体积为VB1-APC1M=2VB1-PC1M=2VP-B1C1M
=2×
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查了空间几何体的应用问题,解题时应根据题意,画出对应的几何图形,结合图形解答问题,是中档题目.

练习册系列答案
相关题目