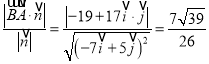��Ŀ����
����Ŀ��������ƽ��ֱ������ϵ�����ǿ��Զ���ƽ��б����ϵ��������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����
����![]() ��������ͬ��ĵ�λ�����ֱ���
��������ͬ��ĵ�λ�����ֱ���![]() ����
����![]() ��
��![]() �ļн�Ϊ
�ļн�Ϊ![]() ������
������![]() ����ƽ��������������������ƽ���ڵ�����
����ƽ��������������������ƽ���ڵ�����![]() ������Ψһ����ʵ����
������Ψһ����ʵ����![]() ��ʹ��
��ʹ��![]() ����
����![]() ������
������![]() ��б����ϵ
��б����ϵ![]() �е����꣬Ҳ��������
�е����꣬Ҳ��������![]() ��б����ϵ
��б����ϵ![]() �е����ꡣ��ƽ��б����ϵ�ڣ�ֱ�ߵķ������������������㷽��ʽ���̡�һ��ʽ���̵ȸ�����ƽ��ֱ������ϵ����Ӧ��������ͬ��ʽ���壬��
�е����ꡣ��ƽ��б����ϵ�ڣ�ֱ�ߵķ������������������㷽��ʽ���̡�һ��ʽ���̵ȸ�����ƽ��ֱ������ϵ����Ӧ��������ͬ��ʽ���壬��![]() ʱ������
ʱ������![]() ��ʾб����ϵ��һ������(2,1)���ҷ�������Ϊ(4,-5)��ֱ�ߡ�
��ʾб����ϵ��һ������(2,1)���ҷ�������Ϊ(4,-5)��ֱ�ߡ�
��1����![]() ��
��![]() ����
����![]() ��
��![]() �ļн�Ϊ��ǣ���ʵ��m��ȡֵ��Χ��
�ļн�Ϊ��ǣ���ʵ��m��ȡֵ��Χ��
��2����![]() ����֪��
����֪��![]() ��ֱ��
��ֱ��![]() ����l��һ���������������A��ֱ��l�ľ��롣
����l��һ���������������A��ֱ��l�ľ��롣
���𰸡���1��![]() ��2��
��2��![]() .
.
��������
��1������������![]() ������
������![]() �н�Ϊ��ǣ��ó�
�н�Ϊ��ǣ��ó�![]() >0���Ӷ��ó�
>0���Ӷ��ó�![]()
![]() ͬ��ʱ���ɵõ�����t��ʹ��
ͬ��ʱ���ɵõ�����t��ʹ��![]() ���Ӷ����m��12���������ɵó�ʵ��m��ȡֵ��Χ��
���Ӷ����m��12���������ɵó�ʵ��m��ȡֵ��Χ��
��2�����Ȱ�ֱ��l�ķ���д��![]() ���Ӷ��ó�ֱ��l�ķ�������Ϊ
���Ӷ��ó�ֱ��l�ķ�������Ϊ![]() �����跨����Ϊ
�����跨����Ϊ![]() ������
������![]() ���ɵõ�5a+7b��0���Ӷ���ȡa����7��b��5���Ӷ��ó�l��һ��������Ϊ
���ɵõ�5a+7b��0���Ӷ���ȡa����7��b��5���Ӷ��ó�l��һ��������Ϊ![]() ;
;
����ȡֱ��l��һ��B��0��2�����Ӷ��õ�![]() ���Ӷ��ó���A��ֱ��l�ľ���Ϊ
���Ӷ��ó���A��ֱ��l�ľ���Ϊ![]() .
.
��1������֪![]() ����
����![]() =2m+6+��12+m��(
=2m+6+��12+m��(![]() )=
)=![]() ����
����![]() ;
;
��![]() ��
��![]() ͬ�����������t��ʹ��
ͬ�����������t��ʹ��![]() ,
,
��![]() ��
��![]() ��ƽ�еã�
��ƽ�еã�![]() ��m=12��
��m=12��
������Ϊ![]() ;
;
��2���ٷ��̿ɱ���Ϊ![]() ����������Ϊ
����������Ϊ![]() ,
,
�跨����Ϊ![]() ����
����![]() ��
��![]() ,
,
��![]() ;
;
��ȡֱ��![]() ��һ��B(0,2)����
��һ��B(0,2)����![]() ������Ϊ
������Ϊ