题目内容
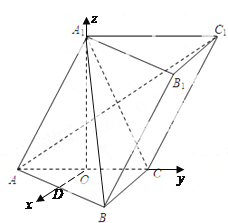
【题目】用空间向量解决下列问题：如图，在斜三棱柱
中， 
是
的中点， 
⊥平面
， 
， 
．
（1）求证： 
；
（2）求二面角
的余弦值．
【答案】（1）证明见解析；（2）
.
【解析】试题分析：先由线面垂直的性质可证明
，由三角形中位线定理及
，可证明
，从而可以以
为原点，直线
、
、
分别为
、
、
轴建立空间直角坐标系. （1）分别求出
， 
，可得
，从而可得
；（2）分别求出平面
的一个法向量
与平面
的一个法向量
，由空间向量夹角余弦公式可得结果.
试题解析：取
的中点
，连结
，
⊥平面
， 
， 
平面，
， 
，
、
分别是
、
的中点， 
，
又
， 
，
所以，可以以
为原点，直线
、
、
分别为
、
、
轴建立空间直角坐标系，设
，于是
， 
， 
，
， 
，
（1）
， 
，
，即
.
（2）由（1）知
， 
， 
， 
,设
是平面
的一个法向量，由
，
，取
，得
， 
， 
，
设
是平面
的一个法向量，由
，
，取
，得
，
， 
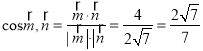， 又因为二面角
为锐二面角，所以，二面角的余弦值为
．
练习册系列答案
相关题目
【题目】某学校高一年级有学生
名，高二年级有
学生名.现用分层抽样方法（按高一年级、高二年级分二层）从该校的学生中抽取
名学生，调查他们的数学学习能力.
（Ⅰ）高一年级学生中和高二年级学生中各抽取多少学生？
（Ⅱ）通过一系列的测试，得到这名学生的数学能力值.分别如表一和表二
表一：
高一年级 |
|
|
|
|
|
人数 |
|
|
|
|
|
表二：
高二年级 |
|
|
|
|
|
人数 |
|
|
|
|
|
①确定
，并在答题纸上完成频率分布直方图；
②分别估计该校高一年级学生和高二年级学生的数学能力值的平均数（同一组中的数据用该组区间的中点值作代表）；
③根据已完成的频率分布直方图，指出该校高一年级学生和高二年级学生的数学能力值分布特点的不同之处（不用计算，通过观察直方图直接回答结论）