��Ŀ����
����Ŀ����ijѧУ�����꼶��![]() �������������ȡ
�������������ȡ![]() ���������ߣ��������ֱ���ѧ������ȫ������
���������ߣ��������ֱ���ѧ������ȫ������![]() ��
��![]() ֮�䣬��������������·�ʽ�ֳɰ��飬��һ��
֮�䣬��������������·�ʽ�ֳɰ��飬��һ��![]() ���ڶ���
���ڶ���![]() ��
��![]() ���ڰ���
���ڰ���![]() ����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�����һ����ڰ���������ͬ�������顢�����顢�ڰ����������ι��ɵȲ����У�
����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�����һ����ڰ���������ͬ�������顢�����顢�ڰ����������ι��ɵȲ����У�

��![]() ����������ѧУ�����꼶ȫ����������
����������ѧУ�����꼶ȫ����������![]() ���ϣ���
���ϣ���![]() ����������
����������
��![]() ��������顢�������Ƶ�ʲ���������Ƶ�ʷֲ�ֱ��ͼ����Ǧ����ͼ�������Ա���ڣ���
��������顢�������Ƶ�ʲ���������Ƶ�ʷֲ�ֱ��ͼ����Ǧ����ͼ�������Ա���ڣ���
��![]() �������������ڵ�����͵ڰ�������������������ȡ���������������ǵ����߷ֱ�Ϊ
�������������ڵ�����͵ڰ�������������������ȡ���������������ǵ����߷ֱ�Ϊ![]() ��
��![]() ��������
��������![]() ���¼����ʣ�
���¼����ʣ�
���𰸡���1��9�ˣ���2������������3��![]()
�������������������1����Ƶ�ʷֲ�ֱ��ͼ�ɵ�ǰ����Ƶ�ʣ������ɵú�����Ƶ�ʺ��������ֿɵú�������������ɵ�ƽ�����ߣ�
��2���ú������![]() ���ɵ�Ƶ�ʷֲ�ֱ��ͼ��
���ɵ�Ƶ�ʷֲ�ֱ��ͼ��
��3���ɣ�![]() ��֪������
��֪������![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() �ˣ�
�ˣ�
��![]() ��
��![]() ��
��![]() ��
��![]() ������Ϊ
������Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
��Ϊ![]() ��
��![]() �����оٿɵ��ܵĻ����¼���15��������¼���
�����оٿɵ��ܵĻ����¼���15��������¼���![]() ���������Ļ����¼�������6+1=7���ɸ��ʹ�ʽ�ɵã�
���������Ļ����¼�������6+1=7���ɸ��ʹ�ʽ�ɵã�
�����������![]() ����Ƶ�ʷֲ�ֱ��ͼ֪��
����Ƶ�ʷֲ�ֱ��ͼ֪��
ǰ����Ƶ��Ϊ![]() ��
��
������Ƶ��Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
����ѧУ��������������![]() ���ϣ���
���ϣ���![]() ��������Ϊ
��������Ϊ![]() �ˣ�
�ˣ�
��![]() ����Ƶ�ʷֲ�ֱ��ͼ�õڰ���Ƶ��Ϊ
����Ƶ�ʷֲ�ֱ��ͼ�õڰ���Ƶ��Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
�����������Ϊ![]() �������������Ϊ
�������������Ϊ![]() ����
����![]() ������
������![]() ��
��
������������Ϊ![]() ��������������Ϊ
��������������Ϊ![]() �ˣ�Ƶ�ʷֱ�Ϊ
�ˣ�Ƶ�ʷֱ�Ϊ![]() ��
��![]() ��
��
Ƶ�ʳ������ֱ����![]() ��
��![]() ����ͼ��
����ͼ��
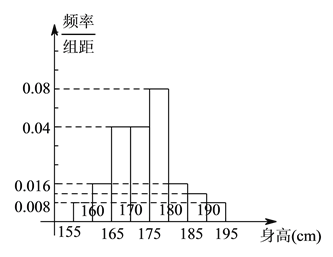
��![]() ���ɣ�
���ɣ�![]() ��֪������
��֪������![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() �ˣ�
�ˣ�
��![]() ��
��![]() ��
��![]() ��
��![]() ������Ϊ
������Ϊ![]() ������Ϊ
������Ϊ![]() �ˣ�
�ˣ�
��Ϊ![]() ��
��![]() ��
��
��![]() ��
��![]() ʱ����
ʱ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����������
�����������
��![]() ��
��![]() ʱ����
ʱ����![]() ��һ�������
��һ�������
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��ʱ��
��ʱ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �������
�������
���Ի����¼�������Ϊ![]() �֣�
�֣�
�¼�![]() �������Ļ����¼�������
�������Ļ����¼�������![]() �֣���
�֣���![]() ��
��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�����Ŀ��ijУΪ�˽��һʵ������ѧ�ɼ�,���ó�������ķ�ʽ,��ȡ��![]() λѧ���ڵ�һѧ��ĩ����ѧ�ɼ�����,����ͳ�ƽ�����±���
λѧ���ڵ�һѧ��ĩ����ѧ�ɼ�����,����ͳ�ƽ�����±���
���� | Ƶ�� | Ƶ�� |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
�ϼ� |
|
|
(1)��![]() ��ֵ��ʵ�����ѧƽ���ֵĹ���ֵ��
��ֵ��ʵ�����ѧƽ���ֵĹ���ֵ��
(2)����÷ֲ�����ķ�������ѧ�ɼ�С��![]() �ֵ�ѧ���г�ȡ
�ֵ�ѧ���г�ȡ![]() ��ѧ��,�ٴ���
��ѧ��,�ٴ���![]() ��ѧ����ѡ
��ѧ����ѡ![]() ��,��������һ��ѧ������ѧ�ɼ�����
��,��������һ��ѧ������ѧ�ɼ�����![]() �ĸ���.
�ĸ���.

