Question

【题目】已知向量 满足 ，若M为AB的中点，并且 ，则λ+μ的最大值是（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图所示， ∵向量 满足 =1， ，
不妨取A（1，0），B（0，1）．
∵M为AB的中点，
∴M ．
∵ =λ（1，0）+μ（0，1）=（λ，μ）．
∵ ，
∴ =1，
设 ，μ= +sinθ，θ∈[0，2π）．
则λ+μ=1+sinθ+cosθ=1+ ，当 =1时取等号．
∴λ+μ的最大值是1+ ．
故选：B．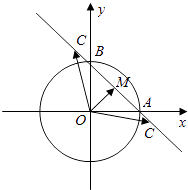

向量 满足 =1， ，不妨取A（1，0），B（0，1）．利用中点坐标公式可得M ．由 =（λ，μ）．及其 ，可得 =1，换元 ，μ= +sinθ，θ∈[0，2π）．即可得出．