题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,坐标原点为
两点,坐标原点为![]() ,且
,且![]() 12.
12.
(Ⅰ)求抛物线的方程;
(Ⅱ)当以![]() 为直径的圆的面积为
为直径的圆的面积为![]() 时,求
时,求![]() 的面积
的面积![]() 的值.
的值.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ) ![]() 的面积为4.
的面积为4.
【解析】试题分析:(I)将![]() 代入
代入![]() ,利用韦达定理可得,
,利用韦达定理可得, ![]() ,利用
,利用![]() ,可得
,可得![]() ,代入即可得到
,代入即可得到![]() 的值;(Ⅱ)根据(I)中
的值;(Ⅱ)根据(I)中![]() 的值,将
的值,将![]() 化为
化为![]() ,可得到
,可得到![]() 的式子,由直径
的式子,由直径![]() ,解方程可求出
,解方程可求出![]() 的值,进而可求出
的值,进而可求出![]() 的面积
的面积![]() 的值.
的值.
试题解析:(I)设![]() ,代入
,代入![]() ,得
,得![]()
设点![]() ,则
,则![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() .
.
所以抛物线的方程为![]() .
.
(Ⅱ)由(I)![]() 化为
化为![]() ,则
,则![]() .
.
又![]() ,
,
因为以![]() 为直径的圆的面积为
为直径的圆的面积为![]() ,
,
所以圆的半径为4,直径![]() .
.
则![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() ,得
,得![]() (舍去)或
(舍去)或![]() ,解得
,解得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为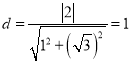 ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为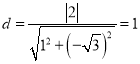 ,且
,且![]() ,所以
,所以![]() 的面积为
的面积为![]() .
.
综上, ![]() 的面积为4.
的面积为4.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目

