Question

2．若实数x，y满足不等式组$\left\{\begin{array}{l}{x+y-2≥0}\\{x≤3}\\{y≤4}\end{array}\right.$，则z=y-x的最小值为-4．

Answer 1

分析 首先画出不等式组表示的平面区域，再根据目标函数的几何意义求最小值．

解答 解：不等式组表示的区域如图：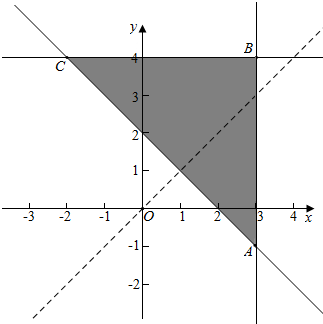
．
设z=y-x，则y=x+z，所以z 的最小值是过A（3，-1）与直线y=x平行的直线在y轴的截距，为-1-3=-4．
故答案为：-4．

点评 本题考查了简单线性规划的问题，首先正确画出平面区域，然后根据目标函数的几何意义求最值．