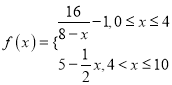题目内容
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程__________.
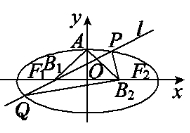
【答案】x+2y+2=0和x-2y+2=0
【解析】
试题分析:设所求椭圆的标准方程为![]() (a>b>0),右焦点为F2(c,0).
(a>b>0),右焦点为F2(c,0).
因△AB1B2是直角三角形,又|AB1|=|AB2|,故∠B1AB2为直角,因此|OA|=|OB2|,得b=![]() .结合c2=a2-b2得4b2=a2-b2,故a2=5b2,c2=4b2,所以离心率e=
.结合c2=a2-b2得4b2=a2-b2,故a2=5b2,c2=4b2,所以离心率e=![]() =
=![]() .
.
在Rt△AB1B2中,OA⊥B1B2,故
S△AB1B2=![]() ·|B1B2|·|OA|=|OB2|·|OA|=
·|B1B2|·|OA|=|OB2|·|OA|=![]() ·b=b2.
·b=b2.
由题设条件S△AB1B2=4,得b2=4,从而a2=5b2=20.
因此所求椭圆的标准方程为:![]() .
.
![]() ,
,![]() 。由题意知直线l的倾斜角不为0,故可设直线的方程为:
。由题意知直线l的倾斜角不为0,故可设直线的方程为: ![]() 。
。
代入椭圆方程得![]() 。
。
设![]() ,
,![]() ,则
,则 ![]() 是上面方程的两根,因此,
是上面方程的两根,因此,![]() 。又,
。又,![]() ,所以由
,所以由 ![]() ,得
,得 ![]() ,即
,即 ![]() ,解得
,解得![]() 。所以满足条件的直线有两条,其方程分别为
。所以满足条件的直线有两条,其方程分别为![]() 和
和![]() 。
。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
【题目】铁矿石A和B的含铁率为![]() ,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表:
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).