题目内容
1.已知直线x-y-1=0与椭圆(n-1)x2+ny2-n(n-1)=0(n>1)交于A、B两点,若以AB为直径的圆过椭圆的左焦点F,求实数的n值.分析 求出F的坐标,直线方程代入椭圆方程并整理,利用韦达定理,结合以AB为直径的圆过椭圆的焦点F,利用向量的数量积公式,即可求得结论.
解答 解:由题意,椭圆方程为:$\frac{{x}^{2}}{n}$+$\frac{{y}^{2}}{n-1}$=1,
∴c=$\sqrt{n-(n-1)}$=1,∴F(-1,0),
将直线y=x-1代入椭圆 $\frac{{x}^{2}}{n}$+$\frac{{y}^{2}}{n-1}$=1并整理,
得:(2n-1)x2-2nx+2n-n2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=$\frac{2n}{2n-1}$,x1x2=$\frac{2n-{n}^{2}}{2n-1}$,
∴y1y2=(x1-1)(x2-1)=$\frac{-{n}^{2}+2n-1}{2n-1}$,
∵以AB为直径的圆过椭圆的左焦点F(-1,0),
∴$\overrightarrow{FA}$•$\overrightarrow{FB}$=0,即(x1+1,y1)•(x2+1,y2)=0,
∴$\frac{2n-{n}^{2}}{2n-1}$+$\frac{2n}{2n-1}$+1+$\frac{-{n}^{2}+2n-1}{2n-1}$=0,
∴n2-4n+1=0,
∴n=2±$\sqrt{3}$,
又∵n>1
∴n=2+$\sqrt{3}$.
点评 本题考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,考查学生分析解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.P(x0,y0)是圆x2+y2=R2内异于圆心的一点,则直线x0x+y0y=R2与圆x2+y2=R2的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
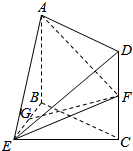 如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.
如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.