题目内容
16.已知函数y=ax+b(a>1,b>0)的图象经过点P(1,3),则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为$\frac{9}{2}$.分析 函数y=ax+b(b>0)的图象经过点P(1,3),可得3=a+b,a>1,b>0.即(a-1)+b=2.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵函数y=ax+b(b>0)的图象经过点P(1,3),
∴3=a+b,a>1,b>0.
∴(a-1)+b=2.
∴$\frac{4}{a-1}$+$\frac{1}{b}$=$\frac{1}{2}$(a-1+b)($\frac{4}{a-1}$+$\frac{1}{b}$)
=$\frac{1}{2}$(5+$\frac{4b}{a-1}$+$\frac{a-1}{b}$)≥$\frac{1}{2}$(5+2$\sqrt{\frac{4b}{a-1}•\frac{a-1}{b}}$)=$\frac{9}{2}$,
当且仅当a-1=2b=$\frac{4}{3}$时取等号.
故答案为:$\frac{9}{2}$.
点评 本题考查了函数的图象与性质、“乘1法”与基本不等式的性质,属于基础题.

练习册系列答案
相关题目
8.函数f(x)=ax2+x-lnx存在极值点,且只有一个极值点大于3,则实数a的取值范围是( )
| A. | (-$\frac{1}{8}$,0)∪(0,+∞) | B. | (-$\frac{1}{9}$,0) | C. | (-$\frac{1}{9}$,0)∪(0,+∞) | D. | (-$\frac{1}{9}$,+∞) |
6.当x∈[-1,t]时,函数f(x)=|x-2|+|5-x|的值域为[3,9],则实数t的取值范围是( )
| A. | [2,8] | B. | [2,4] | C. | [4,8] | D. | [-1,5] |
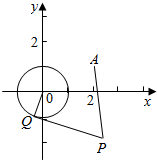 已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.