题目内容
【题目】如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点. 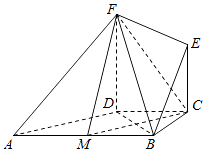
(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
【答案】
(1)证明:∵FD⊥底面ABCD,∴FD⊥AD,FD⊥BD
∵AF=BF,∴△ADF≌△BDF,∴AD=BD,
连接DM,则DM⊥AB,
∵AB∥CD,∠BCD=90°,
∴四边形BCDM是正方形,∴BD⊥CM,
∵DF⊥CM,∴CM⊥平面BDF.
(2)解:当CN=1,即N是CE的中点时,MN∥平面BEF.
证明如下:
过N作NO∥EF,交ED于O,连结MO,
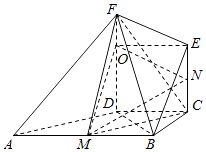
∵EC∥FD,∴四边形EFON是平行四边形,
∵EC=2,FD=3,∴OF=1,∴OD=2,
连结OE,则OE∥DC∥MB,且OE=DC=MB,
∴四边形BMOE是平行四边形,则OM∥BE,又OM∩ON=O,
∴平面OMN∥平面BEF,
∵MN平面OMN,∴MN∥平面BEF.
【解析】(1)推导出四边形BCDM是正方形,从而BD⊥CM,又DF⊥CM,由此能证明CM⊥平面BDF.(2)过N作NO∥EF,交EF于O,连结MO,则四边形EFON是平行四边形,连结OE,则四边形BMON是平行四边形,由此能推导出N是CE的中点时,MN∥平面BEF.
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目