题目内容
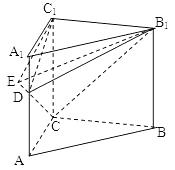
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=BC=2AC=2. (Ⅰ)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(Ⅱ)在AA1上是否存在一点D,使得二面角B1﹣CD﹣C1的大小为60°.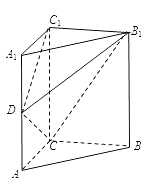
【答案】解法一:(Ⅰ)证明:∵∠A1C1B1=∠ACB=90° ∴B1C1⊥A1C1
又由直三棱柱性质知B1C1⊥CC1∴B1C1⊥平面ACC1A1 .
∴B1C1⊥CD
由AA1=BC=2AC=2,D为AA1中点,可知 ![]() ,
,
∴DC2+DC12=CC12=4即CD⊥DC1
又B1C1⊥CD∴CD⊥平面B1C1D
又CD平面B1CD
故平面B1CD⊥平面B1C1D
(Ⅱ)解:当 ![]() 时二面角B1﹣CD﹣C1的大小为60°.
时二面角B1﹣CD﹣C1的大小为60°.
假设在AA1上存在一点D满足题意,
由(Ⅰ)可知B1C1⊥平面ACC1A1 .
如图,在平面ACC1A1内过C1作C1E⊥CD,交CD或延长线或于E,连EB1 , 则EB1⊥CD
所以∠B1EC1为二面角B1﹣CD﹣C1的平面角
∴∠B1EC1=60°
由B1C1=2知, ![]()
设AD=x,则 ![]()
∵△DCC1的面积为1∴ ![]()
解得 ![]() ,即
,即 ![]()
∴在AA1上存在一点D满足题意
解法二:
(Ⅰ)如图,以C为原点,CA、CB、CC1
所在直线为x、y、z轴建立空间直角坐标系.
则C(0,0,0),A(1,0,0),B1(0,2,2),C1(0,0,2),D(1,0,1).
即 ![]()
由 ![]() 得
得 ![]()
由 ![]() 得
得 ![]()
又DC1∩C1B=C1
∴CD⊥平面B1C1D又CD平面B1CD
∴平面B1CD⊥平面B1C1D
(Ⅱ)当 ![]() 时二面角B1﹣CD﹣C1的大小为60°.
时二面角B1﹣CD﹣C1的大小为60°.
设AD=a,则D点坐标为(1,0,a),![]()
设平面B1CD的法向量为 ![]()
则由 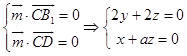 令z=﹣1
令z=﹣1
得 ![]()
又∵ 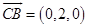 为平面C1CD的法向量
为平面C1CD的法向量
则由 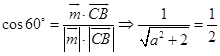
解得 ![]() ,故
,故 ![]() .
.
∴在AA1上存在一点D满足题意
【解析】
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.

 名校课堂系列答案
名校课堂系列答案【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n的值;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级不相同的概率.